от классических построений к модернистско-постмодернистскому синтезу – тема научной статьи по социологическим наукам читайте бесплатно текст научно-исследовательской работы в электронной библиотеке КиберЛенинка
Ю.Ю. Комлев,
доктор социологических наук, профессор (КЮИ МВД России)
ТЕОРИИ ДЕВИАНТНОГО ПОВЕДЕНИЯ. ОТ КЛАССИЧЕСКИХ ПОСТРОЕНИЙ К МОДЕРНИСТСКО-ПОСТМОДЕРНИСТСКОМУ
СИНТЕЗУ
В статье рассмотрены различные подходы к изучению негативной девиантности, структурированы объективистские и субъективистские теории девиантного поведения, раскрыт эвристический потенциал интегративной девиантологии.
Проблематика девиантного поведения в современном обществе — объект постоянного внимания исследователей: социологов, психологов, криминологов. Негативная девиантность и контроль над ее проявлениями исследуются в новых условиях глобализации и стратификации, урбанизации и миграции — противоречивого, кризисного развития «ультрасовременного капитализма». Одним из системообразующих факторов девиантизации общества в современных условиях является его структуризация по критерию «включенность/исклю-ченность» (inclusive/exclusive). Понятие «исключение» (exclusion) появилось во французской социологии второй половины ХХ века как характеристика лиц, оказавшихся на обочине экономического прогресса в условиях «новой бедности».
Негативная девиантность и контроль над ее проявлениями исследуются в новых условиях глобализации и стратификации, урбанизации и миграции — противоречивого, кризисного развития «ультрасовременного капитализма». Одним из системообразующих факторов девиантизации общества в современных условиях является его структуризация по критерию «включенность/исклю-ченность» (inclusive/exclusive). Понятие «исключение» (exclusion) появилось во французской социологии второй половины ХХ века как характеристика лиц, оказавшихся на обочине экономического прогресса в условиях «новой бедности».
В контексте стратификации западных обществ метакод «включенность/исклю-ченность» в настоящих условиях характеризует нарастающий разрыв между увеличивающимся благосостоянием одних и «никому не нужными» другими. Особенность в том, что исключение в экономически развитых странах происходит постепенно: путем накопления трудностей, разрыва социальных связей, дисквалификации, кризиса идентичности, роста девиантности.
изошло на рубеже XXI века взрывообразно: в результате шоковой терапии по Гайдару и приватизации по Чубайсу, череды последовавших рыночных преобразований, образования олигархии и государственно-бюрократического капитализма. И сегодня в нашей стране бедные беднеют все больше, богатые становятся все богаче, при этом все члены общества охвачены плоской шкалой подоходного налога.
Особенно пагубно стратификация общества по основанию «включен-ность/исключенность» отражается на ювенальной среде. «Исключенные» подростки и молодые люди нередко оказываются беспризорными, совершают не только акты уличного хулиганства, обычные кражи, но и более латентные социально опасные преступления (изнасилования, грабежи, разбои, кражи, вымогательства, акты вандализма и экстремизма, преступления на почве ненависти и ксенофобии). В среде исключенных без эффективного социального контроля наряду с «прерывистыми» девиантными карьерами растет риск карьер «интенсивных» на пути рецидивизма и профессионализации преступности, существенно сужается сфера конструктивной активности подростков и молодых людей.
з
По данным Росстата, подростками и молодыми люди в возрасте от 14 до 29 лет включительно совершаются сотни тысяч социально опасных преступлений. Доля этой возрастной группы составе лиц, совершивших преступления, составляет более 50%. Разнообразие и рост масштабов проявлений негативной девиантности, особенно преступности в среде подростков и молодежи, тревожит общественность. Несмотря на некоторое снижение числа несовершеннолетних в составе лиц, совершивших преступления, социологические опросы показывают, что большая часть населения страны (около 60%) считает делинквентность представителей этой группы гораздо более опасной, чем «взрослую преступность».[1]
Наряду с криминальным поведением получают все более массовое распространение саморазрушающие формы девиантности в молодежной среде: алкоголизм и наркотизм. Начиная с 1990 года, наркотизация в России, по оценке С. Г.Олькова, стала развиваться с ускорением по экспоненциальному закону. По статистическим данным, уровень заболеваемости наркоманией среди подростков в нашей стране приблизительно в 2 раза выше, токсикоманией — приблизительно в 8 раз выше, чем среди населения в целом. При этом многие отечественные исследователи фиксируют продолжающееся «омоложение» наркопотребления (Е.А.Кошкина, Н.А.Сиро-та,2001; Ю.Ю.Комлев,2005; М.Е.Поздня-кова,2007). Изменить девиантную биографию, встать на путь исправления в условиях ригористичного российского менталитета, определенной дисфункционально-сти институтов социализации и социального контроля для многих молодых людей
Г.Олькова, стала развиваться с ускорением по экспоненциальному закону. По статистическим данным, уровень заболеваемости наркоманией среди подростков в нашей стране приблизительно в 2 раза выше, токсикоманией — приблизительно в 8 раз выше, чем среди населения в целом. При этом многие отечественные исследователи фиксируют продолжающееся «омоложение» наркопотребления (Е.А.Кошкина, Н.А.Сиро-та,2001; Ю.Ю.Комлев,2005; М.Е.Поздня-кова,2007). Изменить девиантную биографию, встать на путь исправления в условиях ригористичного российского менталитета, определенной дисфункционально-сти институтов социализации и социального контроля для многих молодых людей
— перспектива из числа маловероятных.
Очевидно, что проблематика девиантного и особенно делинквентного поведения на современном этапе развития российского общества, стратифицирующегося по критерию «включенность/
исключенность», нуждается в ос-
новательном научном анализе, качественно выполнить который невозможно в рамках только юридической, педагогиче-
ской, психологической или традиционной позитивистски ориентированной социологической науки. В развитых странах эта предметная сфера концентрируется в интегративном междисциплинарном предметном поле девиантологии или социологии девиантного поведения (sociology of deviant behavior). Благодаря зарубежным де-виантоло-гическим исследованиям накоплен бесценный теоретический материал и опыт его практического применения в практике социального контроля. К сожалению, для значительного числа отечественных криминологов и правоведов деви-антология — все еще терра инкогнита.
В развитых странах эта предметная сфера концентрируется в интегративном междисциплинарном предметном поле девиантологии или социологии девиантного поведения (sociology of deviant behavior). Благодаря зарубежным де-виантоло-гическим исследованиям накоплен бесценный теоретический материал и опыт его практического применения в практике социального контроля. К сожалению, для значительного числа отечественных криминологов и правоведов деви-антология — все еще терра инкогнита.
Исследования девиантологов-теорети-ков опираются как на классическое методологическое наследие обществоведов прошлого, так и на постклассическую, постмодернистскую, интегративную традицию социологического описания девиантности.
 Маркса. Маркс первым в XIX столетии обратил внимание на социально-классовую природу преступности и противодействие ей с социальнополитических позиций. Как известно, его научные взгляды формировались во многом под впечатлением «зверств первоначального накопления» капитала: обострения социального неравенства, конфликтности, роста преступности и других социальных отклонений в европейских городах.
Маркса. Маркс первым в XIX столетии обратил внимание на социально-классовую природу преступности и противодействие ей с социальнополитических позиций. Как известно, его научные взгляды формировались во многом под впечатлением «зверств первоначального накопления» капитала: обострения социального неравенства, конфликтности, роста преступности и других социальных отклонений в европейских городах.К.Маркс и Ф.Энгельс, другие теоретики марксизма определили методологические рамки идеологически ориентированного анализа феномена преступности как «родимого пятна капитализма». Преступность в буржуазном обществе, считал Маркс, -неустранимое явление. По Марксу, «подобно праву, преступление… коренится в тех же условиях, что и существующее гос-подство».[2,с.232] Ф.Энгельс в работе «Положение рабочего класса в Англии» называет преступление «наиболее грубой и самой бесплодной формой… возмущения».
Описывая преступность как протест рабочего класса против капиталистов в форме бесплодной классовой борьбы, Энгельс находит причины социальных отклонений, прежде всего, в экономических условиях современного ему буржуазного общества.
Конфликтологический подход в изучении девиантности получил дальнейшее развитие в рамках постклассической социологии ХХ века. Особую лепту в теоретический анализ девиантного поведения и социального контроля над ним внесли: У.Миллер, Дж.Рейман, С.Спитцер, М.Кол-вин, С.Торстен, О.Терк, Р.Куинни, У.Бон-гер, Г.Руше, О.Хирхаймер и другие социологи как немарксистской, так и неомарксистской ориентации.
Среди девиантологических работ неомарксистов для анализа российской преступности особенно продуктивна теория радикальной криминологии, разработанная Ричардом Куинни (р.1934). Куинни обосновал влияние политического конфликта между господствующим классом и неимущими на формирование девиантного поведения в современных условиях. Еще в книге «Социальная реальность и преступление» (1975) девиантолог, критически оценивая капитализм, определяет его классовую природу как общую причину современной преступности.
В работе «Класс, государство и преступность» (1980) Р.Куинни предложил оригинальную типологию преступного поведения, которая вполне отражает распределение форм преступного поведения и в России с ее государственно-бюрократиче-
ским капитализмом. Так, согласно Куинни, «преступность приспособления» в виде краж, грабежей, убийств и изнасилований распространена в среде рабочих, пострадавших от капиталистической системы; «преступность сопротивления», по его мнению, включает бессознательную реакцию угнетенных «синих воротничков» против эксплуатации; «преступность доминирования и подавления», состоящая в коррупции, откатах, характерна для представителей правящего класса «белых воротничков» и элиты.
В книге «Критика узаконенного порядка: контроль преступности в капиталистическом обществе»(1994) Куинни подчеркивает, что противозаконное поведение власть предержащих во многом не пресекается правосудием. В сфере экономики, управления и контроля это касается, в частности, таких деликтов, как: сокрытие доходов от налогообложения, обман потребителей, коррупция и злоупотребление политической властью. Причем по отношению к люмпенизированным слоям населения уголовное преследование за преступления распространяется в полной мере. Правовые нормы в этой связи не есть результат социального консенсуса. Уголовное законодательство и правоприменение в рыночном обществе рассчитаны на обеспечение господства класса капиталистов, это инструменты эксплуатации угнетенных социальных групп и слоев.
Позитивистский анализ девиантного поведения, социального порядка и стабильности в рамках объективистской традиции был заложен в классических работах функционалиста Э. Дюркгейма. Дюркгейм считал, что социальный порядок как упорядоченность социальных действий индивидов и групп обеспечивается влиянием духовных, социокультурных факторов, способствующих интеграции общества.[4] Ученый обосновал объективность, «нормальность» социальных отклонений. Согласно Дюркгейму, преступность не является социальной патологией — это один из факторов общественного здоровья и неотъемлемая часть любого общества. [3] Преступность существует во
Дюркгейма. Дюркгейм считал, что социальный порядок как упорядоченность социальных действий индивидов и групп обеспечивается влиянием духовных, социокультурных факторов, способствующих интеграции общества.[4] Ученый обосновал объективность, «нормальность» социальных отклонений. Согласно Дюркгейму, преступность не является социальной патологией — это один из факторов общественного здоровья и неотъемлемая часть любого общества. [3] Преступность существует во
всех типах обществ. Она функциональна, поскольку усиливает солидарность группы, объединяя людей в отношении негативной оценки преступлений. Дюркгейм доказал, что преступность как социальная проблема неискоренима. Однако, поскольку она может принимать ненормальные формы, ей можно и нужно противодействовать средствами социального контроля: ограничивать рост и
трансформировать структуру преступности.
Дюркгейм разработал концепцию аномии (anomie), понимая ее как состояние общества, характеризующееся ценностнонормативным вакуумом, разрывом в преемственности социальных и правовых норм. Аномия, согласно Дюркгейму, развивается в переходных быстро меняющихся обществах, что влечет за собой статистически значимый всплеск различных видов девиантного поведения.
Аномия, согласно Дюркгейму, развивается в переходных быстро меняющихся обществах, что влечет за собой статистически значимый всплеск различных видов девиантного поведения.
Теоретические положения из социологии девиантного поведения Э.Дюркгейма в области понимания преступности, аномии, путей обеспечения социальной интеграции, порядка, солидарности и социального регулирования во многом предопределили в своей основе облик современной системы формального полицейского социального контроля в развитых капиталистических странах.
Классик структурного функционализма Т.Парсонс, развивая дюркгеймовскую перспективу объективистского анализа девиантности, выделил при обосновании социального порядка роль социализации, инте-риоризации и легитимизации норм и ценностей (таких, как: неприкосновенность человеческой жизни, частной собственности и т.п.).[5]
Функционалист Р. Мертон, описывая аномию в условиях стабильного рыночного общества, показал, что «отклоняющееся от нормы поведение может быть расценено как симптом несогласованности между определяемыми культурой устремлениями и социально организованными средствами их удовлетворения».[6,с.401] Аномия подталкивает многих людей к использованию незаконных средств обогащения (инноваторство и ритуализм), либо
Мертон, описывая аномию в условиях стабильного рыночного общества, показал, что «отклоняющееся от нормы поведение может быть расценено как симптом несогласованности между определяемыми культурой устремлениями и социально организованными средствами их удовлетворения».[6,с.401] Аномия подталкивает многих людей к использованию незаконных средств обогащения (инноваторство и ритуализм), либо
делает их беспомощными, подавленными (ретретизм), либо стимулирует к экстремизму и терроризму (бунтарство). Мертон обратил внимание на доминирующий корыстный характер преступности при капитализме. По его мнению, люди часто, даже имея таланты, прибегают к незаконным средствам (рэкет, спекуляция, мошенничество, сокрытие доходов от налогообложения, компьютерные преступления). Этот тезис во многом находит подтверждение и в современном российском обществе. Так, по данным уральского социолога В.Г. Попова, современная молодежь чаще всего «сталкивается» с корыстными преступлениями, такими, как воровство (45%), вымогательство денег (35%), разбой (15%), мошенничество (14%). [7,с.73]
[7,с.73]
Концепция аномии получила развитие в постклассической теории блокирования идеалов и фрустрации статуса А.Коэна, где в качестве главных детерминант девиантности рассматриваются социокультурные и статусно-ролевые факторы девиантной адаптации. Аномический анализ развили Р.Кловард и Л.Олин в теории нелигитим-ных возможностей. По мнению Кловарда и Олина, рост вероятности деликтов со стороны деклассированных индивидов больше зависит от возможности их доступа к незаконным средствам для достижения материального успеха и высокого социального статуса. В ситуации, где такие возможности реально могут быть реализованы, молодые люди из необеспеченных семей дают выход своей аномической фрустрации в тех или иных формах групповых делинквентных реакций (криминально ори-ентированн ые, конфликтно-ориентированные и ретритистски-ориентированные шайки), каждая из которых обеспечивается определенным типом делинквентной субкультуры.
В рамках классической бихевиористско-психологической парадигмы социальный порядок и девиантное поведение исследуются с субъективистских позиций. Акцент делается на индивидуально-психологической стороне этих общественных явлений, на символических аспектах социального взаимодействия. Как известно,
Акцент делается на индивидуально-психологической стороне этих общественных явлений, на символических аспектах социального взаимодействия. Как известно,
предтечей субъективистской перспективы в девиантологии был Г.Тард, который опирался на законы подражания при объяснении девиантности и механизмов сплочения общества. В качестве важного фактора социального контроля он одним из первых обратил внимание на возможности социализации личности, на отношения, возникающие между людьми при передаче социального опыта с помощью психологических механизмов. [8]
Фундаментальный вклад в субъективистский анализ феноменов девиантности внес М.Вебер, который превыше всего ставил индивида, причиной развития общества называл культурные ценности. В работе «Протестантская этика и дух капитализма» Вебер показал, каким образом разобщенные между собой действия тысяч предпринимателей и наемных работников создали капитализм — общественную систему огромной сложности с необычайно развитой социальной структурой. Недостаточное освоение норм трудовой этики и проявления девиантности, по Веберу, — это не божья кара, а результат определенных накопившихся, аккумулированных социальных практик, при которых труд плохо оплачивается, работа плохо организована и в силу ежедневных страданий лишена ценностных результатов.
Недостаточное освоение норм трудовой этики и проявления девиантности, по Веберу, — это не божья кара, а результат определенных накопившихся, аккумулированных социальных практик, при которых труд плохо оплачивается, работа плохо организована и в силу ежедневных страданий лишена ценностных результатов.
Собственно психологические интерпретации девиантности в рамках классической субъективистской традиции продолжили
З.Фрейд, Э.Эриксон, Э.Фромм и др. Так, психоаналитический подход З.Фрейда к объяснению девиации покоится на том положении, что человек асоциален по природе и в основе своей представляет неуправляемое, импульсивное социальное животное. Поэтому наличие социальных ограничений необходимо для контроля над его агрессивным, отклоняющимся поведением.
По Фрейду, если все три компонента личности «Ид», «Эго» и «Супер-Эго» действуют сбалансированно, то человек ведет нормальную жизнь, сублимирует. Если «Эго» и «Супер-Эго» выстроены неадекватно в структуре личности, то их запреты не блокируют активизацию инстинктов в
Если «Эго» и «Супер-Эго» выстроены неадекватно в структуре личности, то их запреты не блокируют активизацию инстинктов в
бессознательном. Отсюда следует агрессия и девиантность. По образному выражению немецкого криминолога Г.И.Шнайдера, «преступление — это результат неудачи «Эго» в его попытках удержать под контролем агрессивность, ненависть и фруст-рацию».[9,с.72]
Субъективистские интерпретации девиантности получили дальнейшее развитие в рамках символического интеракционизма в первой половине XX века. Трудами
Ч.Кули и Дж.Мида, И Гофмана и др. было доказано, что личность формируется в результате интеракций с ближайшей социальной средой, осваивая артикулируемые ею требования, правила, нормы — в итоге девиантность подавляется внутренним самоконтролем индивида. Так, по мысли И.Гофмана, социальный порядок формируется в повседневном социальном взаимодействии через соблюдение неписанных и не всегда осознаваемых индивидом правил поведения. Сторонники символического интеракционизма и социального конструктивизма считают, что люди своими действиями конструируют социальную реальность и структуры общества, в том числе систему социального контроля, социальные нормы и девиантность.
Сторонники символического интеракционизма и социального конструктивизма считают, что люди своими действиями конструируют социальную реальность и структуры общества, в том числе систему социального контроля, социальные нормы и девиантность.
Исследования девиантности с позиций символического интеракционизма в по-стклассический период получили наиболее яркое развитие в теориях стигматизации Г.Бекера, Е.Лемерта, Ф.Зака, Э.Шура.
Концептуально теория стигмы (клеймения, лейблов) базируется на двух основных положениях. Во-первых, отклоняющееся поведение следует интерпретировать не как нарушение социальной нормы, признак предрасположенности индивида или качество социального действия, а как результат его символического определения, наклеивания девиантного ярлыка в результате социальной реакции. Поэтому в теории стигматизации особое значение придается силе слова и реакции общества на поведение людей. Во-вторых, «клеймение» порождает и усиливает девиантность. В этом смысле отклоняющееся поведение есть ответ индивида на стигматизацию, который ведет к вторичному от-
Во-вторых, «клеймение» порождает и усиливает девиантность. В этом смысле отклоняющееся поведение есть ответ индивида на стигматизацию, который ведет к вторичному от-
клонению, в ходе чего формируется девиантная идентичность.
Теория лейблов объясняет лишь вторичное отклонение, рецидивизм, процесс формирования девиантной карьеры под воздействием чрезмерного социального контроля, но не этиологию первичного отклонения. Тем не менее, ее эвристический потенциал достаточно высок, чтобы объяснить рост рецидивизма в современном российском обществе, особенно в молодежной среде. Как известно, по статистическим данным МВД России, при общем снижении объема преступности в стране количество рецидивных преступлений в 2010 году возросло на 40%. В структуре рецидивных преступлений половину составляют тяжкие и особо тяжкие, более 60% от всей рецидивной преступности приходится на кражи, грабежи, разбои и хулиганство — составы, создающие наибольшие угрозы и беспокойство для общества в целом и для каждого его члена в отдельности. При этом самый высокий процент рецидива зафиксирован в возрастной группе от 22 до 24 лет.[10] Заметим, что каждое третье преступление совершается лицами, имеющими стигму судимости.
При этом самый высокий процент рецидива зафиксирован в возрастной группе от 22 до 24 лет.[10] Заметим, что каждое третье преступление совершается лицами, имеющими стигму судимости.
В девиантологии эпохи модерн в рамках объективистской или субъективистской традиции девиантность и преступность описываются позитивистски типично определенно, без использования элементов рассуждения (диалога), дискурса. С развитием постмодернизма — детища второй половины XX века его основоположниками французскими философами Ж-Ф.Лиотаром и М.Фуко изменились и представления о девиантном поведении. Как известно, постмодернизм отражает переход общества от эпохи модерна к состоянию постмодерна, от классовой структуры к обществу фрагментарного типа. Постмодернизм характеризуется интенсивным скептицизмом по отношению к науке, возможностям человеческого разума, релятивизацией всех знаний. Постмодернизм ставит под сомнение веру в возможность познания и преобразования мира. Для философии постмодернизма присущи рефлексивность, пастиш (смешение стилей, заим-
Для философии постмодернизма присущи рефлексивность, пастиш (смешение стилей, заим-
ствованных из различных контекстов). Постмодернист и криминолог Э.Янг в работе «Imagining Crime. Textual Outlaws and Criminal Conversations» (1996) переосмысливает криминологические тексты, проводит дискурсивный анализ, исследует роль языка, символов и метафор в создании образов преступного поведения.
Релятивны и сконструированы с позиций постмодернизма социальные нормы, ценности, девиантность и преступность, а также само общество как их источник. По мысли Г.Барака, «преступления — это рекурсивная продукция, однообразные действия, которые стали частью исторического и культурного общения, достигшие относительной стабильности в определенном времени и пространстве.[11,р.219]
В итоге девиантология и криминология постмодерна определяют преступление на контрасте объяснения этого явления в модернизме и постмодернизме, на отказе от внешней причинности и жесткого рационализма. Преступность и контроль над ней мыслятся посмодернистам как неопределенные, взаимосвязанные, относительные, динамические конструкции. Тем самым постмодернизм проблематизирует представления о феноменах девиантности и преступности, современном социальном порядке и контроле над отклоняющимся поведением.
Преступность и контроль над ней мыслятся посмодернистам как неопределенные, взаимосвязанные, относительные, динамические конструкции. Тем самым постмодернизм проблематизирует представления о феноменах девиантности и преступности, современном социальном порядке и контроле над отклоняющимся поведением.
Постклассический и, особенно, постмодернистский дискурс в социальной науке и девиантологии, исходя из релятивизации знаний, открыли путь к новым направлениям исследований девиантности. В результате девиантологами было выдвинуто много новых гипотез и теорий, объясняющих природу девиантности на постсовре-менном этапе развития общества.
Анализ новых оригинальных зарубежных работ по теории девиации весьма затруднителен. Во всяком случае, достаточно сложно провести грань между современными теориями, связанными как с классическими концепциями девиантности, так и постклассическими. Зарубежные авторы активно интегрируют положения классических и постклассических теорий в собственных концептуальных построе-
ниях. Наиболее полное изложение новых идей и подходов в девиантологии и криминологии содержат, с нашей точки зрения, труд Делоса Кейли «Deviant Behav-ior»(1996), работы Рональда Айкерса «Criminological theories: introduction and evaluation»(1997) и Грега Барака «Integrating Criminologies» (1998).
Наиболее полное изложение новых идей и подходов в девиантологии и криминологии содержат, с нашей точки зрения, труд Делоса Кейли «Deviant Behav-ior»(1996), работы Рональда Айкерса «Criminological theories: introduction and evaluation»(1997) и Грега Барака «Integrating Criminologies» (1998).
Анализ англоязычных и немногих отечественных работ позволяет по крупицам собрать материал о состоянии и направлениях развития современной девиантологической мысли за рубежом. Обобщение положений из публикаций англоязычных де-виантологов, переведенных на кафедре философии, политологии, социологии и психологии при участии курсантов КЮИ МВД России, позволяет дать краткий обзор современных направлений девиантологической и криминологической мысли.
Феноменологическое направление традиционно противостоит позитивистским теориям девиантности. Феноменология основную свою задачу видит в анализе и описании повседневной жизни — жизненного мира и связанных с ним состояний сознания. Его сторонники в девиантологии
Его сторонники в девиантологии
— П.Филмер, М.Филипсон, Д.Уолш. Феноменологи развивают идеи конвенциональ-ности преступности и девиантности в целом. По их мнению, отклонение — не внутренне присущее тому или иному действию качество, а следствие соотнесения действий с правилами и применением санкций к нарушителю. Социальное отклонение — это в значительной степени приписываемый статус, в нем фиксируются не только поступки самого отклоняющегося индивида, но и действия окружающих его людей. Отсюда происходит штампование «преступников», их конструирование.
Феминизм (М.Маерс, Д.Клейн, Р.Саймон, Ф.Адлер) в девиантологии опирается на анализ различий по биологическому (секс) и социальному (гендер) полу. В рамках феминизма развиваются либеральные, радикальные и марксистские течения. Сторонники феминизма не удовлетворены традиционными позитивистскими теориями девиантности, поскольку те ориентированы на объяснение преступного
поведения только со стороны мужчин. Они считают, что все существующие биологические и психологические теории, теории аномии, социального контроля, дифференциальной ассоциации, стигматизации, дезорганизации и социального научения созданы для того, чтобы объяснять преступность мужчин и проверялись только на мужском населении.[12,p.197] Определенные части этих теорий, по мнению теоретиков феминизма, полезны, но в целом они не пригодны для объяснения феномена женской преступности. При этом хорошо развитого исключительно феминистского объяснения девиантности в зарубежных источниках найти не удается.
Они считают, что все существующие биологические и психологические теории, теории аномии, социального контроля, дифференциальной ассоциации, стигматизации, дезорганизации и социального научения созданы для того, чтобы объяснять преступность мужчин и проверялись только на мужском населении.[12,p.197] Определенные части этих теорий, по мнению теоретиков феминизма, полезны, но в целом они не пригодны для объяснения феномена женской преступности. При этом хорошо развитого исключительно феминистского объяснения девиантности в зарубежных источниках найти не удается.
Либеральный феминизм причину преступности видит в социализации по гендерному основанию (в ее специфике). Женской преступности препятствуют гендерные нормы, более плотный социальный контроль (готовность рисковать поощряется у мальчиков и пресекается у девочек), физическая слабость и уязвимость женщин по сравнению с мужчинами, репродуктивносексуальные отличия женщин и мужчин.
Таким образом, девиантологи-феми-нисты при изучении женской преступности и девиантности считают ключевыми факторами гендерные различия и возраст, которые другие теории игнорируют. Наряду с поло-ролевыми факторами, они отводят весьма важную роль в объяснении отклоняющегося поведения женщин фоновой патриархальной структурой, которая пронизывает все стороны жизни современного общества.
Наряду с поло-ролевыми факторами, они отводят весьма важную роль в объяснении отклоняющегося поведения женщин фоновой патриархальной структурой, которая пронизывает все стороны жизни современного общества.
Современная критическая криминология как направление девиантологической мысли объединяет сторонников левого реализма, миротворческой (аболиционизм) криминологии и конститутивной криминологии. Все эти направления в современной девиантологии занимают критические позиции по отношению к современному западному обществу и его системе криминальной юстиции.
Левый реализм — течение в неомарксистской критической криминологии, выступающее против левого идеализма и ортодоксального марксизма. Его наиболее яр-
кий представитель — британский криминолог Джон Янг. Левые реалисты исходят из того, что не только среди преступников, но и среди жертв преступлений большинство составляют представители низших классов. Они считают, что уличные преступники и преступники из числа служащих -это «революционные солдаты в классовой борьбе».[12,p.179]
Они считают, что уличные преступники и преступники из числа служащих -это «революционные солдаты в классовой борьбе».[12,p.179]
Аболиционизм — миротворческая криминология. Его последователи в США и скандинавских странах Европы (Т.Матисен, Н.Кристи, Х.Пепинский) выступают против современной тюремной системы, предлагая альтернативные меры социального контроля. На смену политики «войны с преступностью», по их мнению, должна прийти политика «мира с преступностью». Рост насильственной преступности в развитых странах вызван эскалацией насилия со стороны государства. Аболиционисты выступают за отказ от института смертной казни и репрессивной полицейской и пенитенциарной системы, предлагая стратегию уменьшения вреда (harm reduction).
Конститутивная криминология, созданная на основе постмодернизма, отвергает поиск причин преступности в объективной реальности и рассматривает ее как продукт «дискурсивных практик» среди преступников, контролеров (полицейских, тюремных надзирателей) и жертв преступлений. С позиций постмодернизма преступность и контроль над ней не могут быть отделены от всеобщего структурного и культурного контекста, в котором они продуцируются. Это положение конститутивной теории активно противостоит традиционной криминологии, которая вырывает из социального и культурного контекстов феномены преступного поведения, анализируя их раздельно.
С позиций постмодернизма преступность и контроль над ней не могут быть отделены от всеобщего структурного и культурного контекста, в котором они продуцируются. Это положение конститутивной теории активно противостоит традиционной криминологии, которая вырывает из социального и культурного контекстов феномены преступного поведения, анализируя их раздельно.
Интегративные теории девиантности. На рубеже XXI века в эпоху «ультрасовременного капитализма» с его новой стратификацией по критерию «включен-ность/исключенность», с качественным ростом неопределенности многих социальных феноменов, с возникновением виртуальной реальности, симулякров и симу-
ляций от девиантности в зарубежной криминологии и девиантологии сложился заказ на новый модернистско-постмо-дерни-стский синтез девиантологических знаний. Интегративная перспектива в теории может указать путь преодоления антагонизма между объективизмом и субъективизмом, между позитивизмом и феноменологией в условиях жесткого диалога и противоборства парадигм. Как полагает Г.Барак, модернистско-постмодернистский синтез лежит в основе, возможно, самого полного объяснения и контроля преступлений.[11] Действительно, детерминация многих современных форм девиантного, делинквентного поведения с позиций только одного теоретического подхода отнюдь не всегда является успешной, а подчас и невозможной. В связи с этим создание интегративных теорий в последние десятилетия на Западе есть результат обобщения, интеграции наиболее удачных положений для объяснения преступности из уже существующих двух и более девиантологических теорий. Так, например, Рональд Айкерс создал свою интегративную теорию «концептуального поглощения» (Conceptual Absorption), привлекая понятийный аппарат из теорий научения и социального контроля. Аналогичным образом рассуждали девиантологи Френк Пирсон и Нейл Уей-нер при создании теории «интегративной структуры» (Integrative Framework). Объяснительная модель этих авторов построена на принципиальной основе теории социального научения с интеграцией концептов из всех наиболее важных макро- и микро-девиантологических теорий в одной «интегративной рамке».
Как полагает Г.Барак, модернистско-постмодернистский синтез лежит в основе, возможно, самого полного объяснения и контроля преступлений.[11] Действительно, детерминация многих современных форм девиантного, делинквентного поведения с позиций только одного теоретического подхода отнюдь не всегда является успешной, а подчас и невозможной. В связи с этим создание интегративных теорий в последние десятилетия на Западе есть результат обобщения, интеграции наиболее удачных положений для объяснения преступности из уже существующих двух и более девиантологических теорий. Так, например, Рональд Айкерс создал свою интегративную теорию «концептуального поглощения» (Conceptual Absorption), привлекая понятийный аппарат из теорий научения и социального контроля. Аналогичным образом рассуждали девиантологи Френк Пирсон и Нейл Уей-нер при создании теории «интегративной структуры» (Integrative Framework). Объяснительная модель этих авторов построена на принципиальной основе теории социального научения с интеграцией концептов из всех наиболее важных макро- и микро-девиантологических теорий в одной «интегративной рамке». Делберт Эллиот разработал интегративную модель на основе объединения концептов из теорий напряжения, социального контроля и социального научения. Аналогичные построения предложили А.Лиска (теория «состязания») и Т.Торнберри («интегративная теория»). Три взаимосвязанных эксперимента по теоретической интеграции осуществлены Р.Сэмпсоном и Дж.Лаубе (1993), Б.Вилой (1994) и Б.Арриго (1995). Эти новейшие теоретические поиски пока-
Делберт Эллиот разработал интегративную модель на основе объединения концептов из теорий напряжения, социального контроля и социального научения. Аналогичные построения предложили А.Лиска (теория «состязания») и Т.Торнберри («интегративная теория»). Три взаимосвязанных эксперимента по теоретической интеграции осуществлены Р.Сэмпсоном и Дж.Лаубе (1993), Б.Вилой (1994) и Б.Арриго (1995). Эти новейшие теоретические поиски пока-
зали перспективность новой полипарадиг-мальной интеграции в девиантологии.
Резюмируя обзор рассмотренных выше положений из классических и посткласси-ческих девиантологических теорий, можно сделать вывод о том, что в условиях процесса «включения/исключения», возросшей социальной обусловленности, сконст-руированности отклоняющегося поведения в современном мире девиантологическая наука лишь приблизилась к объяснению и пониманию природы негативной девиантности. Различные теоретические модели девиантности показывают, что «человек с отклонениями» интересен как продукт определенного общества, его нормативно-
ролевой структуры, культуры и субкультур, конфликтов и «дискурсивных практик», на которые существенное влияние оказывают разнообразные и взаимосвязанные друг с другом факторы. Девиантность и преступность, социальный контроль над отклонениями не могут быть отделены от всеобщего структурного и культурного контекстов, в которых они продуцируются. Девиантологическое знание релятивно, но оно — надежный ориентир для поиска путей отказа от девиантных карьер, повышения эффективности социального контроля в интересах российского общества и государства
Девиантность и преступность, социальный контроль над отклонениями не могут быть отделены от всеобщего структурного и культурного контекстов, в которых они продуцируются. Девиантологическое знание релятивно, но оно — надежный ориентир для поиска путей отказа от девиантных карьер, повышения эффективности социального контроля в интересах российского общества и государства
ЛИТЕРАТУРА
1.Комлев Ю.Ю. Теория рестриктивного социального контроля. Казань: КЮИ МВД Рос-сии,2009.
2. Маркс К., Энгельс Ф. Немецкая идеология// К.Маркс, Ф.Энгельс. Соч.Т.3.
3.Комлев Ю.Ю., Сафиуллин Н.Х. Социология девиантного поведения. Казань: КЮИ МВД России,2006.
4. Сорокин П.А. Человек. Цивилизация. Общество. М.,1992.
5. Парсонс Т. Система современных обществ. М.,1997.
Парсонс Т. Система современных обществ. М.,1997.
6. Мертон Р.К. Социальная структура и аномия//Социология преступности. М., 1966.
7.Попов В.Г. Молодежь в сфере криминогенного влияния//Социол. исслед.1998. №5.
8. Тард Г. Законы подражания.СПб.,1999.
9. Шнайдер Г.И. Криминология. М.,1994.
10. Петров И. В России резко выросло количество рецидивных преступлений// RBCDAILY от
30.03.2011 [Электронный ресурс] — Доступно из ULR:
http://www.rbcdaily.ru/2011/03/30/focus/562949979958708
11. Barak G.Integrating criminologies. Allyn & Bacon.1998.
12. Akers.R.L. Criminological Theories: introduction and evalution-2nd ed. Los Angeles,1997.
Akers.R.L. Criminological Theories: introduction and evalution-2nd ed. Los Angeles,1997.
Социологические теории девиантного поведения
Социологические теории девиантного поведения
В современном научном дискурсе выделяют следующие социологические теории девиантого поведения:
- теория аномии Эмиля Дюркгейма;
- теория девиации Роберта Мертона;
- теория культурного переноса или подражания Габриэля Тарда;
- теория дифференциальной ассоциации Эдвина Г. Сазерленда;
- марксистская теория конфликта;
- теория стигматизации.
Особенности социологических теорий девиантного поведения
Теория аномии французского социолога Э.Дюркгейма основывается на утверждение о том, что в обществе, находящемся в состоянии разложения ценностной системы, обусловленным общим общественным упадком, люди обнаруживают, что им сложно ориентироваться среди отсутствия определенной системы социальных норм. В условиях стремительных социальных изменений, люди не понимают, какие именно социальные ожидания существуют в данный момент, что определяет сложности с согласованием своих действий и действующих правил. Прежние социальные нормы перестают быть актуальными, а новые социальные нормы слишком пространны, и не сформулированы настолько, чтобы служить ценностным ориентиром в стратегии поведения людей.
В условиях стремительных социальных изменений, люди не понимают, какие именно социальные ожидания существуют в данный момент, что определяет сложности с согласованием своих действий и действующих правил. Прежние социальные нормы перестают быть актуальными, а новые социальные нормы слишком пространны, и не сформулированы настолько, чтобы служить ценностным ориентиром в стратегии поведения людей.
Помощь со студенческой работой на тему
Социологические теории девиантного поведения
Американский социолог Роберт Мертон предпринял попытку продолжить теорию аномии Эмиля Дюркгейма. Анализирую американский общественный опыт, Роберт Мертон установил, что для американцев жизненный успех стал культурной ценностью и целью деятельности. Но отсутствие возможностей к получению доступа к различным ресурсам для достижения успеха склонило людей к девиантному поведению с целью найти другие пути и способы. Так, Роберт Мертон преобразовал дюркгеймовскую теорию: люди склонны к девиации не в том обществе, где социальные нормы отсутствуют, а в том, где нет возможностей следовать существующим.
Теория культурного переноса или подражания французского социолога Габриэля Тарда основывается на идеи повторения. Габриэль Тард считал, что и преступники, и законопослушные люди подражают поведению тех людей, которых они встречали или о которых слышали: так, нарушители подражают преступному поведению. К прочему, люди склоняются к девиатному поведению не только в силу подражания, но и в силу научения, т.к. люди социализируются и инкультурируются в своей среде.
Эдвин Г. Сазерленд разработал теорию дифференциальной ассоциации: человек подражают окружению в той степени, в которой он принадлежит к этому окружению. В контексте девиатного поведения, это означает, что чем раньше человек окажется среди девиантов, тем выше вероятность быть склонным к девиантному поведению.
Теория конфликта: правящие классы эксплуатируют общественные массы, избегая возмездия. Угнетенные классы вынуждены проявлять девиантное поведение, чтобы избежать или переживать эксплуатацию.
Пример 1
Такие явления как алкоголизм, проституция, проявление насилия являются результатом духовного регресса. Он объясняется отчуждением человека от средств производства.
Он объясняется отчуждением человека от средств производства.
Согласно теории стигматизации основой для объяснения девиантного поведения выступает идея конфликта: люди, способные институционально навязывать свои интересы другим людям, также определяют нарушителей актуального общественного порядка, через «навешивание ярлыков». Клеймо оказывает влияние по поступки человека, в некоторых случаях склоняя его к проявлению девиантного поведения.
Замечание 1
Стигма является своеобразным клеймом, определяющим поведение человека.
Согласно теории стигматизации, девиация определяется реакций общества на девиантное поведение. Социальные ожидания от заклейменного человека зачастую подталкивают его к подтверждению данных ожиданий. Поведение, не характерное для навешенного ярлыка, наталкивается на неадекватную общественную реакцию, тем самым затрудняя возможности человека вести нормальный социально одобренный образ жизни.
Страница не найдена |
Страница не найдена | 404. Страница не найдена
Страница не найдена
Архив за месяц
ПнВтСрЧтПтСбВс
21222324252627
282930
12
12
1
3031
12
15161718192021
25262728293031
123
45678910
12
17181920212223
31
2728293031
1
1234
567891011
12
891011121314
11121314151617
28293031
1234
12
12345
6789101112
567891011
12131415161718
19202122232425
3456789
17181920212223
24252627282930
12345
13141516171819
20212223242526
2728293031
15161718192021
22232425262728
2930
Архивы
Июл
Авг
Сен
Окт
Ноя
Дек
Метки
Настройки
для слабовидящих
9.
 5. Социологические теории девиации
5. Социологические теории девиацииПочему люди нарушают общественные нормы? Почему определенные действия характеризуются как девиантные? Этими вопросами интересуются социологи.
Другие науки также занимаются проблемой девиантного поведения, в частности, биология и психология. Однако эти науки пытаются объяснить нарушения правил с точки зрения самих индивидов и их уникальных характеристик. Социологи же пытаются установить социальные факторы возникновения девиации. Исследования доказывают, что отклонение от нормы не является свойством, внутренне присущим человеческому поведению (за исключением случаев медицинской патологии, например, шизофрении). Оно является свойством, обусловленным социальными факторами.Рассмотрим наиболее распространенные социологические подходы к проблеме девиации.
Теория
аномии. Отправной точкой для создания
социологических теорий девиации
послужила теория аномии Э.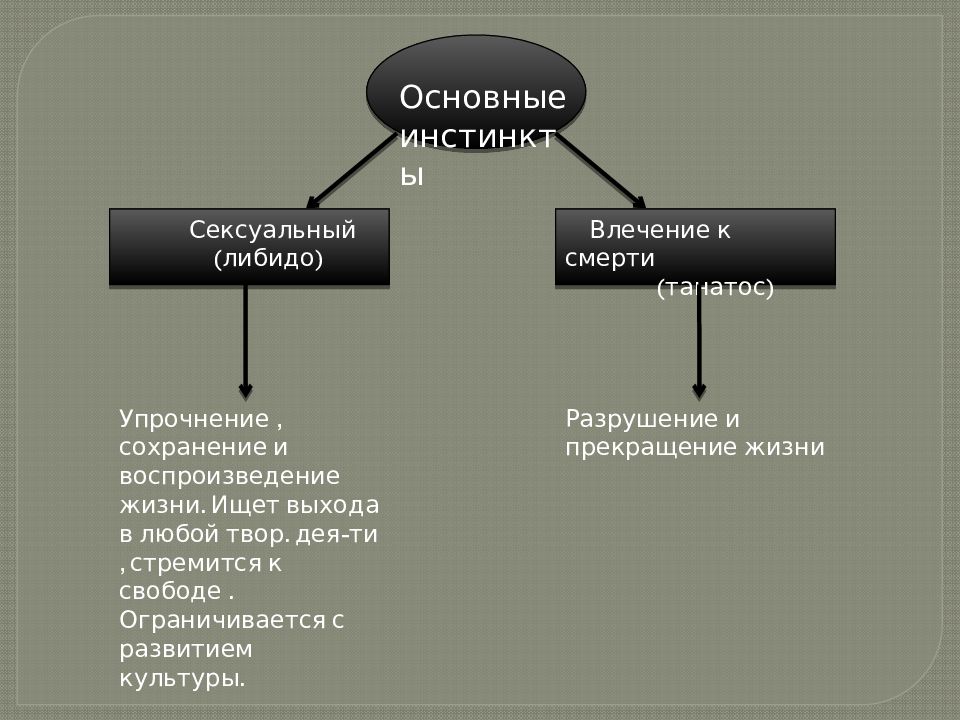 Дюркгейма.Аномия– это общественное состояние,
которое характеризуется разложением
системы ценностей, обусловленным
кризисом всего общества, его социальных
институтов, противоречием между
провозглашенными целями и невозможностью
их реализации для большинства. Люди
обнаруживают, что им трудно координировать
свое поведение в соответствии с нормами,
которые в данный момент становятся
слабыми, неясными или противоречивыми.
Дюркгейма.Аномия– это общественное состояние,
которое характеризуется разложением
системы ценностей, обусловленным
кризисом всего общества, его социальных
институтов, противоречием между
провозглашенными целями и невозможностью
их реализации для большинства. Люди
обнаруживают, что им трудно координировать
свое поведение в соответствии с нормами,
которые в данный момент становятся
слабыми, неясными или противоречивыми.
Таким образом, состояние аномии возникает тогда, когда «старые нормы» уже не представляются подходящими, а новые, зарождающиеся нормы, слишком туманны и нечетко сформулированы, чтобы служить эффективными ориентирами в поведении. В такие периоды можно ожидать резкого возрастания количества случаев девиации.
На
практике дюркгеймовские понятия применил
американский социолог Р. Мертон,
разработавший аномическую теорию
девиации.В основу типологии поведения
людей Мертон кладет отношение личности
к социально одобряемым целям и
институциональным средствам их
достижения.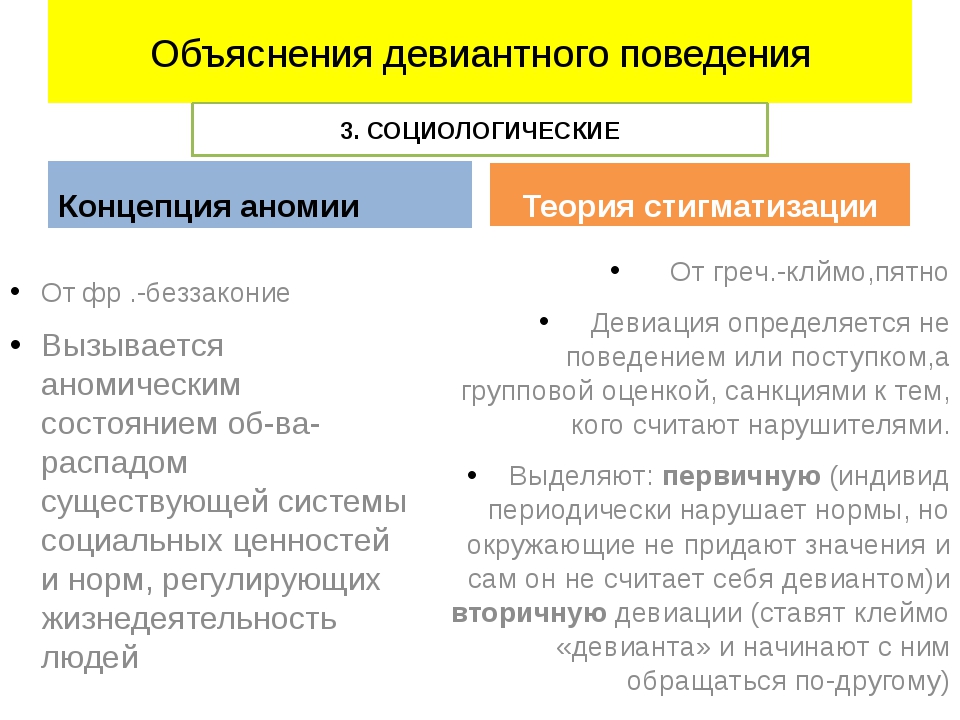 Согласно Мертону, разрыв
между теми и другими как раз и порождает
состояние аномии, порождающее девиацию.
Согласно Мертону, разрыв
между теми и другими как раз и порождает
состояние аномии, порождающее девиацию.
Например, жизненный успех для большинства американцев превратился в культурно признанную цель. Для достижения успеха первостепенными становятся такие факторы, как образование и высокооплачиваемая работа. Проблема заключается в том, что не все американские граждане имеют одинаковый доступ к средствам достижения успеха в жизни. Поэтому многие предпочитают добиваться престижной цели любыми средствами, включая порочные и преступные.
В соответствии с различными вариантами отношения личности к целям и средствам, выделяется единственный недевиантный тип поведения – конформизм, т.е. принятие личностью и социально одобряемых целей, и институциональных способов их достижения, а также четыре девиантных типа:
Инновация— принятие целей и отрицание традиционных средств их достижения. По Мертону, напряжение между акцентом, который делает американская культура на богатстве, и ограниченной возможностью разбогатеть, порождает воровство, наркоторговлю и прочую уличную преступность, особенно среди бедноты.

Так, печально известный гангстер Аль Капоне в чем-то был вполне традиционной фигурой: он гнался за славой и удачей, составляющими самую суть «американской мечты». Но, как и многие представители меньшинств, которым не удалось открыть дверь, ведущую к «законному успеху», Капоне двинулся к вершине своим путем.
Ритуализм— отвержение культурных целей, но принятие одобренных обществом средств. Бюрократы, занимающие низкие ступени на своей служебной лестнице, зная, что они добьются лишь небольшого финансового успеха, цепко держатся за правила, чтобы чувствовать себя уважаемыми людьми и казаться таковыми в глазах посторонних.
Ретрецизм(от англ.retreat– уход, отступление) — отвержение и культурных целей и признанных средств для их достижения при полном бездействии. По сути, индивид «выпадает» из культуры мэйнстрима. Изгоями оказываются некоторые алкоголики, наркоманы и бездомные.
 Их девиантность заключается
в нетрадиционном стиле жизни и, что,
может быть, еще серьезнее — в их
добровольном выборе именно такой жизни.
Их девиантность заключается
в нетрадиционном стиле жизни и, что,
может быть, еще серьезнее — в их
добровольном выборе именно такой жизни.Бунт – отвержение культурных целей, средств и замена их новыми нормами (например, в радикальных общественных движениях). Бунт часто является реакцией на фиаско. Подобно изгоям, бунтари отрицают как культурное определение успеха, так и нормативные средства его достижения. Бунтари идут дальше, формируя контркультуру и отстаивая альтернативы существующему социальному порядку.
Табл.2. Мертоновская типология форм индивидуальной адаптации к аномии
Формы приспособления | Социально одобряемые цели | Институциализированные средства |
Конформизм | + | + |
Инновация | + | — |
Ритуализм | — | + |
Ретритизм | — | — |
Мятеж | +/ — | +/ — |
Примечание: « + » — принятие
« — » — отвержение
«+/ — » — отвержение господствующих ценностей и замена их новыми
Теория
культурного переноса. Ряд
социологов подчеркивает сходство между
способом выработки девиантного поведения
и любого другого поведения. Одним из
первых к такому выводу пришел французский
социолог Габриель Тард. В концеXIXв. Тард сформулировалтеорию подражаниядля объяснения девиантного поведения.
Он утверждал, что преступники, как и
«порядочные люди», имитируют поведение
тех индивидов, с которыми они встречались
в жизни, которых знали или о которых
слышали. Но в отличие от законопослушных
граждан они имитируют поведение
преступников. Таким образом, молодые
люди становятся правонарушителями,
потому что общаются и заводят дружбу с
теми подростками, у которых криминальные
модели поведения уже укоренились.
Ряд
социологов подчеркивает сходство между
способом выработки девиантного поведения
и любого другого поведения. Одним из
первых к такому выводу пришел французский
социолог Габриель Тард. В концеXIXв. Тард сформулировалтеорию подражаниядля объяснения девиантного поведения.
Он утверждал, что преступники, как и
«порядочные люди», имитируют поведение
тех индивидов, с которыми они встречались
в жизни, которых знали или о которых
слышали. Но в отличие от законопослушных
граждан они имитируют поведение
преступников. Таким образом, молодые
люди становятся правонарушителями,
потому что общаются и заводят дружбу с
теми подростками, у которых криминальные
модели поведения уже укоренились.
В
1920 – 1930-е гг. социологи Чикагского
университета установили, что в отдельных
кварталах города уровень преступности
оставался стабильным в течение многих
лет, несмотря на изменения в этническом
составе населения. Был сделан вывод,
что криминальное поведение передается
от одного поколения к другому, а детям
представителей других этнических групп
девиантные модели поведения передаются
от местной молодежи.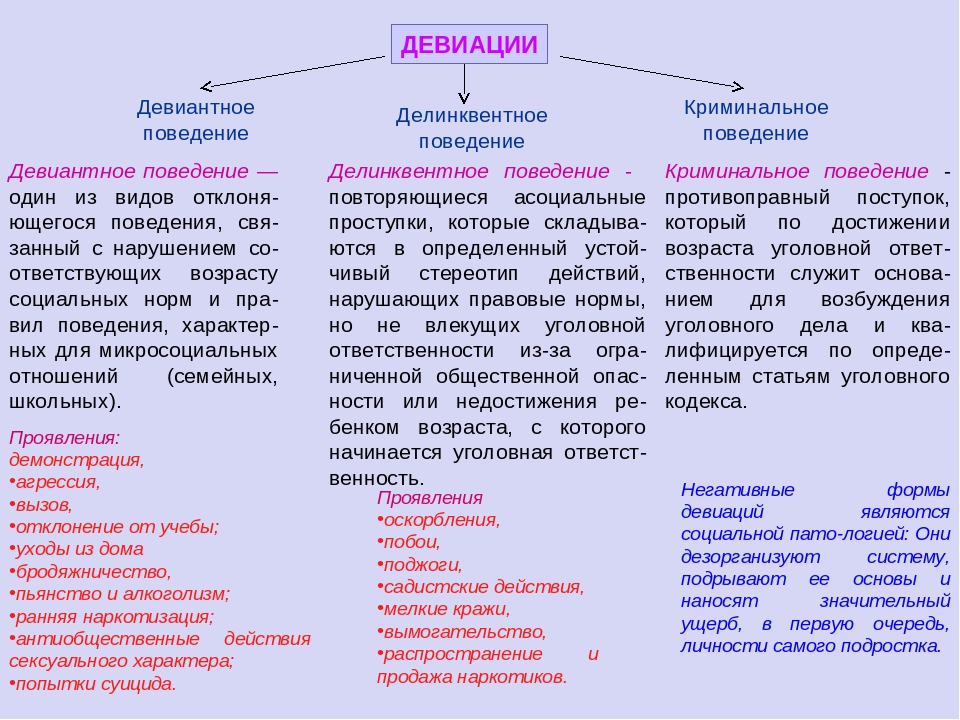
Эдвин Г. Сазерленд, используя выводы чикагских социологов, разработал теорию дифференциальной ассоциации, в соответствии с которой девиантное поведение приобретается на основе не только подражания, но и научения; очень многое зависит от того, чему именно и от кого учатся индивиды. В связи с этим тюремное заключение может привести к явно отрицательным последствиям, если поместить юных правонарушителей в одну камеру с закоренелыми преступниками.
Ее
можно проиллюстрировать исследованием,
посвященным употреблению наркотиков
и алкоголя среди американской молодежи
(Альтерс, 1979). Ответы на вопросники,
розданные в младших и старших классах
средней школы, показали тесную взаимосвязь
между уровнем потребления алкоголя и
наркотиков и степенью, в которой
подобные действия поощрялись группами
сверстников. Исследователи сделали
вывод, что молодые люди берут на вооружение
делинквентные образцы в той мере, в
какой они встречают одобрение и
вознаграждаются за положительное
определение девиантности в противовес
конформности.
Теория навешивания ярлыков(Labelling theory). Эта теория основана на двух основных положениях. Первое состоит в том, что девиантным действием считается не простое нарушение какой-либо нормы, а фактически любое поведение, которое с успехом определяется как девиантное, если на него навешен определенный ярлык, относящейся к этой категории. Другими словами, девиация содержится не столько в самом действии, сколько в реакции других на это действие. Второе положение утверждает, что само навешивание ярлыков продуцирует или распространяет девиацию.
Например, если юный правонарушитель оказался задержанным полицией по обвинению в каком-то проступке, то это может оказать серьезное влияние на всю его дальнейшую жизнь. Так, если раньше он считал себя таким же, как все, то теперь он начинает чувствовать себя особенным.
Ярлык
преступника заставляет человека мнить
себя попавшим в сеть преступных
организаций, то есть обрести криминальную
идентичность. Каждый последующий шаг
по этому пути все более укрепляет у них
ощущение, что они уже стали какими-то
иными – не такими, как все, и не такими
нормальными, как прежде. Иногда такой
процесс называютстигматизацией (от греч.stigma– укол, пятно). В
социологическом смысле стигма – это
социальный признак, дискредитирующий
индивида или целую группу.
Каждый последующий шаг
по этому пути все более укрепляет у них
ощущение, что они уже стали какими-то
иными – не такими, как все, и не такими
нормальными, как прежде. Иногда такой
процесс называютстигматизацией (от греч.stigma– укол, пятно). В
социологическом смысле стигма – это
социальный признак, дискредитирующий
индивида или целую группу.
По мнению Р. Коллинза, преступность создает само общество. В качестве примера он приводит некоторые виды так называемых «преступлений без жертв», когда жертва сама охотно идет на встречу преступнику.
Р.
Коллинз приводит следующий пример:
продажа и приобретение наркотиков не
были преступлением до тех пор, пока не
были приняты законы, превращающие
продажу и приобретение их частными
лицами в серьезное преступление. Общество
в лице государственных органов просто
возвело их в ранг преступления, издав
соответствующие законы. Сегодня, как
ни парадоксально, в сохранении такого
положения больше всего заинтересованы
наркодельцы, поскольку легализация
наркотиков существенно снизила бы их
гигантские прибыли.
Теория конфликта. Основу конфликтологического подхода к теории девиации заложил Карл Маркс. Согласно ей, правящий класс капиталистов эксплуатирует и грабит народные массы и при этом избегает возмездия за свои преступления. Трудящиеся – жертвы капиталистического угнетения – в своей борьбе за выживание вынуждены совершать проступки, которые правящий класс клеймит как преступные. Такие типы девиантного поведения, как алкоголизм, наркомания, проституция и насилие в семье являются продуктами моральной деградации, основанной на беспринципной погоне за наживой и угнетении бедняков, женщин, представителей этнических меньшинств.
Современный
марксистский подход к проблеме девиации
сформулировал Ричард Квинни. Согласно
Квинни, правовая система США отражает
интересы и идеологию правящего
капиталистического класса. По его
мнению, преступление присуще
капиталистической системе. Когда
общество создает социальные проблемы
и не может справиться с ними естественным
образом, оно придумывает и вводит
политику контроля за населением. Следовательно, преступление и уголовное
наказание составляют неотъемлемую
часть более крупных проблем исторического
развития капитализма.
Следовательно, преступление и уголовное
наказание составляют неотъемлемую
часть более крупных проблем исторического
развития капитализма.
Так, многие социологи отмечают, что преступление определяется в основном в терминах ущерба, наносимого собственности (кража со взломом, грабеж, угон автомобилей, вандализм), в то время как корпоративные преступления как бы остаются в тени. ФБР ведет множество дел по фактам убийств, изнасилований, но ни одно государственное агентство не ведет регистрацию преступлений, совершенных корпорациями.
Вместе с тем, следует отметить, что у теории конфликта есть много критиков, подвергающих сомнение научность многих выводов данной теории и предлагающих подвергнуть их более тщательной проверке.
В
заключении следует подчеркнуть, что ни
одна теория объяснения причин девиантного
поведения не является абсолютной и
применимой ко всем случаям девиации.
Каждая высвечивает какой-то один важный
источник отклонения поведения от нормы. А девиантное поведение может принимать
множество форм. Поэтому следует тщательно
анализировать каждую форму девиации
для определения задействованных в ней
специфических факторов.
А девиантное поведение может принимать
множество форм. Поэтому следует тщательно
анализировать каждую форму девиации
для определения задействованных в ней
специфических факторов.
Цели изучения дисциплины | 1.Формирование у студентов представлений о многообразии различных теорий, концепций и направлений социологии девиантного поведения. 2.Объективно оценивать социальную реальность общественного устройства России на различных этапах её развития. Уметь правильно определить причины девиантного поведения. 3.Разбираться в вопросах отклоняющегося поведения, а именно: девиантного поведения, делинкветного поведения, криминального поведения, отклоняющегося трудового поведения, знать их виды и типы. 4.Самостоятельно работать с источниками и литературой по социологии девиантного поведения и проводить сравнительный анализ фактов и событий на основе методов социологического исследования. | Содержание дисциплины | — Исследования девиаций в системе социальных наук: основные категории и понятия. — Теоретические подходы к социологии девиантного поведения. — Типология отклоняющегося поведения. — Виды девиантного поведения. — Проблемы преступности и криминального поведения в современном обществе. — Отклоняющееся трудовое поведение в обществе. — Проблемы социального контроля над девиантным поведением. — Профилактика девиантного поведения. — Социологический мониторинг девиантного поведения в обществе. | Знания, умения и навыки, получаемые в результате изучения дисциплины | ЗНАТЬ Основные отечественные и зарубежные теоретические подходы к феномену девиантности; классификацию и типологию видов отклоняющегося поведения; факторы, обуславливающие генезис девиантного поведения; основные модели девиантного поведения; сущность и основные особенности наиболее распространенных видов и форм девиации; о генезисе представлений о социальных нормах и отклонениях; о сущности, функциях и типологии социальных норм. УМЕТЬ Ориентироваться в многообразии различных теорий, концепций и направлений социологии девиантного поведения; объективно оценивать социальную реальность общественного устройства России на различных этапах её развития. Уметь правильно определить причины девиантного поведения; разбираться в вопросах отклоняющегося поведения, а именно: девиантного поведения, деликветного поведения, криминального поведения, отклоняющегося трудового поведения, знать их виды и типы. Самостоятельно работать с источниками и литературой по социологии девиантного поведения и проводить сравнительные анализы фактов и событий на основе методов социологического исследования. ВЛАДЕТЬ Основами диагностики и измерения девиантного поведения и специфике исследований проявлений девиантности; теоретико-методологическими основами социального регулирования девиантного поведения; способностью использования фундаментальных социологических знаний в практике девиантного поведения. |
3 Теории девиации — Медична соціологія
3 Теории девиации
Биологизаторские теории. Преступное поведение
объясняется биологической предрасположенностью индивида. Один из ярких
представителей этого направления является Ч. Ломброзо, который связывал
склонность к преступному поведению с особым типом внешности и телосложения.
Преступное поведение
объясняется биологической предрасположенностью индивида. Один из ярких
представителей этого направления является Ч. Ломброзо, который связывал
склонность к преступному поведению с особым типом внешности и телосложения.
Теории социального научения. Согласно этим теориям, люди, живущие или воспитывающиеся в группах, где ведущими являются девиантные социальные установки, усваивают негативные формы социального поведения.
Теория аномии. Аномия – это распад норм, регулирующих
социальное взаимодействие. Данная теория была предложена Э. Дюркгеймом. Он
считал, что социальные нормы ограничивают человеческие желания, которые не
знают пределов. В случае, когда влияние норм и правил перестает быть столь
сильным (переходные общества, революции), возрастает количество различного рода
правонарушений. Понятие аномии было расширено Р. Мертоном. Мертон выделил определяемые
культурой цели и институциональные средства их достижения. Общества отличаются
друг от друга степенью, в которой подчеркиваются цели или средства. Если
общества большее значение придают целям, то индивиды могут использовать
незаконные средства для их достижения. Например, если в обществе царит культ
богатства, то человек, имеющий его, будет оцениваться позитивно вне зависимости
от того, какими путями это богатство он добыл.
Общества отличаются
друг от друга степенью, в которой подчеркиваются цели или средства. Если
общества большее значение придают целям, то индивиды могут использовать
незаконные средства для их достижения. Например, если в обществе царит культ
богатства, то человек, имеющий его, будет оцениваться позитивно вне зависимости
от того, какими путями это богатство он добыл.
Теории усвоения культуры. В начале лекции мы рассматривали тот факт, что девиация является относительным понятием – то, что в одной культуре является нормой, в другой оценивается как отклонение. Теории усвоения культуры подчеркивают, что девиантное поведение является результатом социализации в субкультурной группе, где данное поведение является нормальным.
Теория
социальной дезорганизации. Отклоняющееся поведение может возникать в
результате смешения ценностей и норм различных культур. Например, уровень
преступности выше в крупных городах, где проживают люди разных культур, национальностей,
социальных слоев.
Теория социально-экономических факторов. Согласно этой концепции, девиантное поведение возникает в условиях значительных социально-экономических противоречий. При существовании большого социального расслоения и слабой социальной защищенности люди самостоятельно начинают заниматься перераспределением богатства (кражи, грабежи, экономическая преступность).
Теория навешивания ярлыков. Данная теория рассматривает девиацию как результат социальной оценки. В любом обществе есть господствующие социальные группы, которые определяют то или иное поведение как нормальное или отклоняющееся. Например, лица, являющиеся представителями государственной власти, попытки смещения этой власти будут объявлять противозаконными, а их носителей – наказывать. Причина, согласно данной теории, в том, что высшие государственные чиновники не хотят лишаться власти и связанных с ней привилегий.
Ярлык
«девианта» дает его носителю специальный статус. Если окружающие узнают, что
данный человек является гомосексуалистом либо представителем экзотического
религиозного культа, они начинают интерпретировать его поведение в свете новой
информации и относится к нему соответствующим образом, т.е. формируется
девиантная стереотипизация. Е. Гуд выделил пять элементов девиантной
стереотипизации:
Если окружающие узнают, что
данный человек является гомосексуалистом либо представителем экзотического
религиозного культа, они начинают интерпретировать его поведение в свете новой
информации и относится к нему соответствующим образом, т.е. формируется
девиантная стереотипизация. Е. Гуд выделил пять элементов девиантной
стереотипизации:
- преувеличение – окружающие склонны фокусироваться на экстремальных формах девиации. Например, мужской гомосексуализм ассоциируется с женоподобностью. Однако, согласно исследованиям сексологов, существует скрытый гомосексуализм, который внешне никак не проявляется;
- централизация – мнение о том, что девиация играет определяющую роль в жизни человека. Например, спинальный больной может оцениваться как неудачник во всех сферах, исходя из того, что он не может ходить;
- стойкость – зачастую люди исходят из мнения – однажды оступившийся – преступник на всю жизнь;
-
дихотомия – склонность считать, что девиация есть, либо ее нет.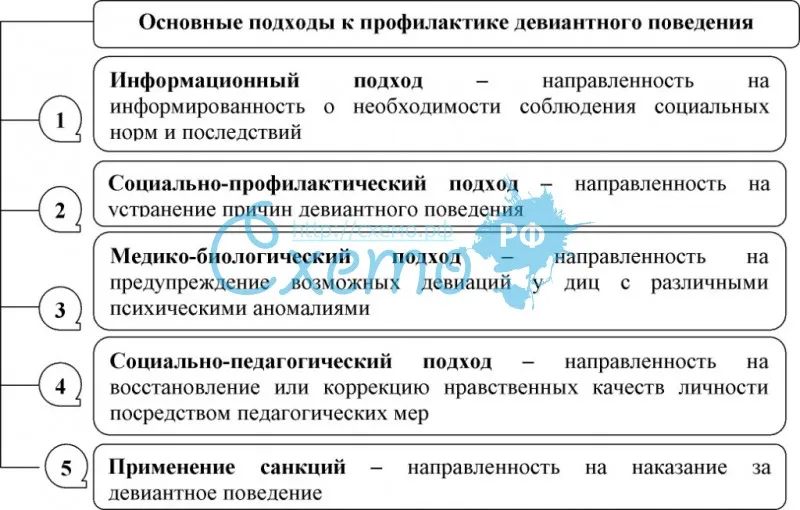 Однако, как
показывают психологические исследования, в большинстве случаев существуют
промежуточные варианты характеров и форм поведения. Ранее уже упоминавшийся
гомосексуализм имеет разную степень выраженности у разных людей;
Однако, как
показывают психологические исследования, в большинстве случаев существуют
промежуточные варианты характеров и форм поведения. Ранее уже упоминавшийся
гомосексуализм имеет разную степень выраженности у разных людей;
- генетическая предрасположенность – мнение о том, что любые отклонения генетически запрограммированы и неизбежно могут проявиться. Однако, анализ специальной литературы показывает, что легкие формы отклонений (шизофрения, психопатия и т.д.) могут успешно компенсироваться. Если окружающие не знают о диагнозе, такой человек будет оцениваться просто как своеобразный и оригинальный.
Теория
наклеивания ярлыков рассматривала также механизмы формирования девиантности.
Если человеку наклеивают ярлык девианта, это может усилить или стимулировать
различные проявления отклонений в поведении. Другими словами, если окружающие
относятся к человеку как к девианту, он начинает своим поведением подтверждать
их ожидания. Подобное поведение Э. Гоффман, один из создателей теории
наклеивания ярлыков, назвал «девиантной карьерой».
Подобное поведение Э. Гоффман, один из создателей теории
наклеивания ярлыков, назвал «девиантной карьерой».
Итак, деятельность любой социальной группы и общества в целом подчиняется определенным нормам. Наличие норм, в свою очередь, заставляет обратить внимание на существование девиаций в обществе. Девиации имеют неоднозначный характер и оказывают разностороннее влияние на общество, как положительное, так и отрицательное. Для регуляции уровня девиаций в обществе используется социальный контроль и социальные санкции.
Контрольные вопросы и задания
1. Какую роль играют в обществе социальные нормы?
2. Приведите примеры социальных норм. Какие критерии для выделения этих норм вы использовали?
3. Объясните, почему социальные девиации одновременно являются относительными и абсолютными. Приведите примеры.
4.
Приведите
примеры позитивных девиаций. Почему общество зачастую относится к ним
негативно?
Почему общество зачастую относится к ним
негативно?
5. Каким образом взаимосвязаны индивидуальные и групповые отклонения?
6. Что такое первичные и вторичные отклонения?
7. Какую роль играют девиации в обществе?
8. Проанализируйте формы социального контроля, выделенные Т. Парсонсом. Приведите примеры.
9. Почему социализация является формой социального контроля?
10. Сравните эффективность позитивных и негативных санкций.
38
Теоретико-методологическое обоснование общей теории девиантности и девиантного поведения
Аннотация
В представленной статье обсуждаются актуальные теоретико-методологические проблемы девиантологии: обосновывается необходимость и возможность выделения общей теории девиантности в междисциплинарное научное направление; раскрываются понятия, образующие предметное поле девиантологии; формулируются основные положения структурно-динамической концепции девиантности и девиантного поведения.
Ключевые слова
девиантология, структурно-динамическая концепция девиантности и девиантного поведения, девиация, нормативно-интегрированная и отклоняющаяся социализация личности, латентная и актуальная девиантность, девиантное поведение, детерминация девиантного поведения
Ссылка для цитирования
Змановская Е.В. Теоретико-методологическое обоснование общей теории девиантности и девиантного поведения // Учёные записки Санкт-Петербургского государственного института психологии и социальной работы. 2008. № 1 (9). С. 133–138.
Список литературы
- Гилинский Я.И. Девиантология (Социология преступности, наркотизма, проституции, самоубийств и других «отклонений»). — СПб., 2004.
- Змановская Е.В. Девиантология (Психология отклоняющегося поведения). — СПб., 2001.
- Змановская Е.В. Девиантология (психология отклоняющегося поведения): Учеб.
 пособие для студентов высших учеб. заведений. — М., 2003.
пособие для студентов высших учеб. заведений. — М., 2003. - Змановская Е.В. и др. Программы и методики социальной реабилитации семей групп «риска»: Научно-методическое пособие // Под ред. Н.М. Платоновой. — СПб., 2002.
- Змановская Е.В. Психология девиантного поведения: структурно-динамический подход. Монография. — СПб., 2005.
- Кудрявцев В.Н. Преступность и нравы переходного общества. — М., 2002.
- Лунеев В.В. Преступность ХХ века. Мировые, региональные и российские тенденции. — М., 1997.
Анализ тепловых волн и периодов холода на основе теории больших отклонений в упрощенной модели общей циркуляции атмосферы
Типичный способ формализации анализа экстремумов для стохастической переменной X вращается вокруг рассмотрения хвоста распределение вероятностей X и определение экстремумов как очень больших (или очень маленьких) событий с длительным временем возврата. Этот момент — как обсуждается ниже — математически очень силен, но в обычных условиях не очень хорошо подходит для изучения, в случае пространственно-временного хаоса, аномально больших или малых событий, которые сохраняются во времени и / или растянуты в пространстве.Постоянные экстремальные климатические явления, такие как волны тепла или похолодания, могут иметь огромное влияние: они влияют не только на здоровье человека, но и на экосистемы; они могут представлять опасность для нашей инфраструктуры и сельскохозяйственных культур и оказывать дестабилизирующее воздействие на целые общества; масштаб ущерба в значительной степени зависит от постоянного характера и пространственного масштаба событий (Истерлинг и др. 2000, Робинсон 2001, ВОЗ 2004, IPCC 2012). Среди наиболее актуальных исторических примеров мы хотели бы упомянуть мега-засуху, сыгравшую важную роль в крахе империи майя (Kennett et al 2012), и повторяющиеся эпизоды сильного похолодания, называемые дзудами, которые привели к к различным волнам миграции кочевого монгольского населения (Fang and Liu 1992, Hvistendahl 2012).
Этот момент — как обсуждается ниже — математически очень силен, но в обычных условиях не очень хорошо подходит для изучения, в случае пространственно-временного хаоса, аномально больших или малых событий, которые сохраняются во времени и / или растянуты в пространстве.Постоянные экстремальные климатические явления, такие как волны тепла или похолодания, могут иметь огромное влияние: они влияют не только на здоровье человека, но и на экосистемы; они могут представлять опасность для нашей инфраструктуры и сельскохозяйственных культур и оказывать дестабилизирующее воздействие на целые общества; масштаб ущерба в значительной степени зависит от постоянного характера и пространственного масштаба событий (Истерлинг и др. 2000, Робинсон 2001, ВОЗ 2004, IPCC 2012). Среди наиболее актуальных исторических примеров мы хотели бы упомянуть мега-засуху, сыгравшую важную роль в крахе империи майя (Kennett et al 2012), и повторяющиеся эпизоды сильного похолодания, называемые дзудами, которые привели к к различным волнам миграции кочевого монгольского населения (Fang and Liu 1992, Hvistendahl 2012).
Волна тепла или похолодания не только длится долго (от нескольких дней до нескольких недель, даже месяцев), но и имеет значительную пространственную протяженность. Например, волны тепла в Европе в 2003 и 2010 годах имели временную и пространственную протяженность от нескольких недель до месяцев и 10 6 км 2 соответственно (Barriopedro et al 2011). Эти устойчивые явления в первую очередь вызваны аномальными синоптическими условиями, а в случае средних широт — ситуациями блокирования атмосферы, поэтому мы говорим о постоянстве в пространстве и времени в больших синоптических масштабах (Vautard и др. 2007, Sillmann ). и др. 2011, Стефанон и др. 2012 г.).На рисунке 1 (a) мы изображаем интенсивность и масштабы аномальной жары 2010 года, а на рисунке 1 (b) мы показываем, как резко возрастает избыточная смертность, наблюдавшаяся во Франции во время аномальной жары 2003 года в результате устойчивых крупных положительных аномалий. температур (Poumadere et al 2005).
температур (Poumadere et al 2005).
Увеличить Уменьшить Сбросить размер изображения
Рисунок 1. Пространственно-временные характеристики волн тепла и их влияние на здоровье.(а) Аномалии температурных максимумов в четырех различных временных масштабах во время аномальной жары 2010 года. Изолинии показывают аномалии, разделенные на стандартное климатологическое отклонение температуры в том же месте в летние дни. Рекордные места обозначены точками. Абсолютные максимумы указаны в верхнем левом углу. Воспроизведено из Barriopedro et al (2011). (b) Число дополнительных смертей во Франции в августе (календарные дни месяца, указанные на оси x ) во время аномальной жары 2003 года.Обратите внимание, что количество ежедневных дополнительных смертей увеличивается день ото дня во время аномальной жары, а затем быстро стремится к нулю. Воспроизведено из Poumadere et al (2005).
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения В климатической системе существует нетривиальная взаимосвязь между пространственным и временным масштабами изменчивости — с большими пространственными масштабами, обычно связанными с более длинными временными масштабами. Эффективный способ представить такую взаимосвязь — использовать так называемые спектры Хаяши (Hayashi 1971, Fraedrich and Boettger 1978, Speranza 1983, Dell’Aquila et al 2005).Существование такой взаимосвязи проистекает из того факта, что можно свободно идентифицировать различные динамические режимы, каждый из которых характеризуется специальным динамическим балансом между силами, действующими на компоненты жидкости (Lucarini et al 2014). Такие балансы можно строго вывести с помощью асимптотического анализа, применяемого к уравнениям Навье – Стокса во вращающейся системе отсчета (Klein, 2010).
Эффективный способ представить такую взаимосвязь — использовать так называемые спектры Хаяши (Hayashi 1971, Fraedrich and Boettger 1978, Speranza 1983, Dell’Aquila et al 2005).Существование такой взаимосвязи проистекает из того факта, что можно свободно идентифицировать различные динамические режимы, каждый из которых характеризуется специальным динамическим балансом между силами, действующими на компоненты жидкости (Lucarini et al 2014). Такие балансы можно строго вывести с помощью асимптотического анализа, применяемого к уравнениям Навье – Стокса во вращающейся системе отсчета (Klein, 2010).
Как хорошо известно, понимание процессов, связанных с синоптическими возмущениями, которые доминируют в изменчивости погоды в средних широтах, прочно основано на теории бароклинной нестабильности (см. Holton (2004)).При рассмотрении явлений, характеризующихся более длинными характерными временными масштабами, ситуация становится значительно менее ясной.
Часто термин «низкочастотная изменчивость» используется для описания обширного диапазона атмосферных процессов, происходящих в масштабе времени от примерно недели до примерно месяца.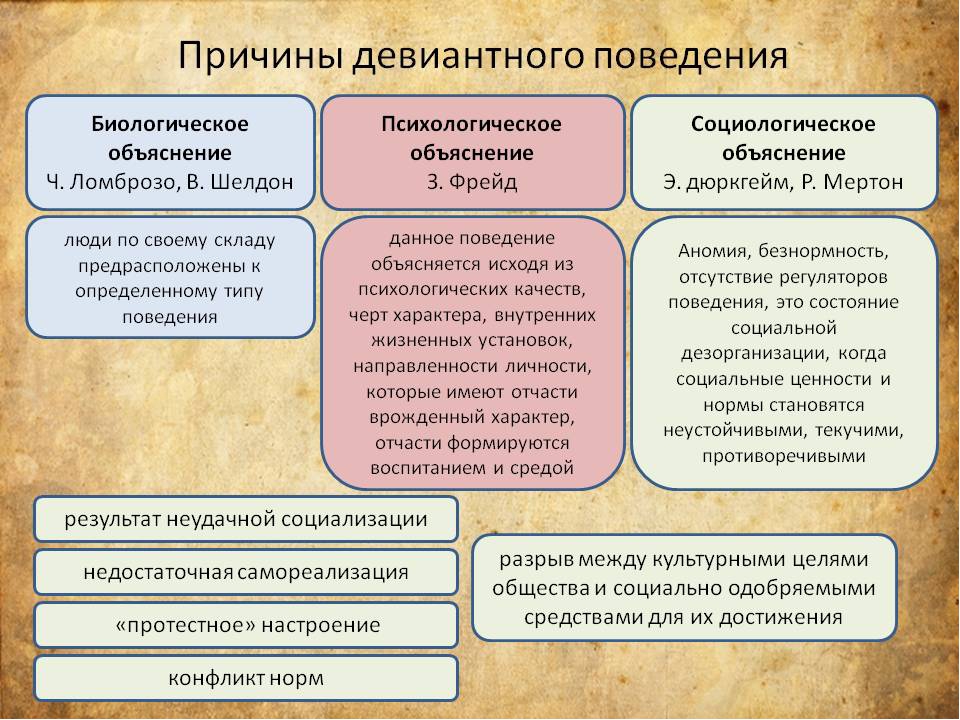 Низкочастотная изменчивость характеризует гораздо большее разнообразие явлений по сравнению с синоптической изменчивостью, и, несмотря на десятилетия усилий с точки зрения теоретических исследований, наблюдений и численного моделирования, полного понимания пока не достигнуто.Устойчивые погодные аномалии, которые могут привести к длительным экстремальным температурам, т. Е. Волнам жары и похолоданиям, связаны с квазистационарными волнами Россби (Sillmann et al 2011, Stefanon et al 2012). Фазовая скорость этих волн зависит от длины волны и всегда направлена на запад, то есть против направления среднего потока в средних широтах. Если длина волны достаточно велика, фазовая скорость волн Россби может стать очень низкой или даже нулевой, что приведет к квазистационарным или стационарным аномальным синоптическим ситуациям — так называемым блокирующим событиям; см. недавний обзор Тибальди и Молтени (2018).
Низкочастотная изменчивость характеризует гораздо большее разнообразие явлений по сравнению с синоптической изменчивостью, и, несмотря на десятилетия усилий с точки зрения теоретических исследований, наблюдений и численного моделирования, полного понимания пока не достигнуто.Устойчивые погодные аномалии, которые могут привести к длительным экстремальным температурам, т. Е. Волнам жары и похолоданиям, связаны с квазистационарными волнами Россби (Sillmann et al 2011, Stefanon et al 2012). Фазовая скорость этих волн зависит от длины волны и всегда направлена на запад, то есть против направления среднего потока в средних широтах. Если длина волны достаточно велика, фазовая скорость волн Россби может стать очень низкой или даже нулевой, что приведет к квазистационарным или стационарным аномальным синоптическим ситуациям — так называемым блокирующим событиям; см. недавний обзор Тибальди и Молтени (2018).
1.1. Математическая основа для экстремальных климатических явлений
1.
 1.1. Теория экстремальных ценностей.
1.1. Теория экстремальных ценностей. Надежная математическая основа для изучения экстремальных значений обеспечивается теорией экстремальных значений. Один из способов построения теории экстремумов в соответствии с процедурой блочных максимумов можно резюмировать следующим образом. Рассматривается последовательность реализаций независимых и одинаково распределенных переменных и берется максимум M m на m таких переменных (Fisher and Tippett 1928, Gnedenko 1943).В качестве альтернативы, экстремальные значения могут быть построены в соответствии с так называемым методом «пик над порогом», рассматривая ту же последовательность переменных, что и раньше, и выбирая значения, превышающие заданный порог и (Balkema and de Haan 1974, Pickands 1975). Оба метода сформулированы в форме предельных законов и основаны на сходимости распределения выбранных экстремальных значений к одному ограничивающему семейству распределений для обширного класса родительских распределений, поскольку каждый рассматривает все более и более экстремальные уровни, т. е.е. для блоков размером м и порог и соответственно. Условие независимости стохастических переменных может быть ослаблено, чтобы включить случай слабо коррелированных переменных (Leadbetter et al 1983), и может быть сформулировано таким образом, чтобы позволить установить законы экстремальных значений для наблюдаемых хаотические динамические системы (Лукарини и др. 2016).
е.е. для блоков размером м и порог и соответственно. Условие независимости стохастических переменных может быть ослаблено, чтобы включить случай слабо коррелированных переменных (Leadbetter et al 1983), и может быть сформулировано таким образом, чтобы позволить установить законы экстремальных значений для наблюдаемых хаотические динамические системы (Лукарини и др. 2016).
Предельное семейство распределений — это обобщенное распределение экстремальных значений в случае метода блочных максимумов и обобщенное распределение Парето в случае подхода пика над порогом.Теорема Пикандса – Балкема – де Хаана гарантирует, что в пределе существует взаимно однозначное соответствие между обобщенным экстремальным значением и обобщенным предельным распределением Парето для данного набора данных, даже если при рассмотрении конечных данных оба подходы отбирают разных кандидатов на крайности (Balkema and de Haan 1974, Pickands 1975). Если предельное обобщенное экстремальное значение или обобщенное распределение Парето существуют и могут быть надежно оценены, можно рассчитать вероятность возникновения событий, более экстремальных, чем любое наблюдаемое событие.Другими словами, можно построить надежные оценки периодов повторяемости для временных диапазонов, превышающих то, что действительно наблюдается. Это указывает на то, что, если применяется предельный закон, предсказательная сила (в статистическом смысле) проявляется для событий с очень низкой вероятностью возникновения. Обратите внимание, что, хотя универсальность проявляется в пределе, скорость, с которой реализуются асимптотические свойства, зависит от процесса, то есть не универсальна (Gálfi et al 2017).
Как ясно следует из приведенного выше обсуждения, статистический анализ, основанный на теории экстремальных ценностей, в принципе чрезвычайно полезен именно для тех заинтересованных сторон, которым необходимо планировать на долгое время вперед, и фактически уже давно применяется в таких областях, как финансы ( Embrechts et al 1997), инженерии (Castillo 1988) и гидрологии (Katz et al 2002).Несколько удивительно, хотя примеры применения, очевидно, можно найти, методы теории экстремальных значений все еще не являются основным подходом для изучения очень интенсивных явлений в исследованиях климата, где более популярно использовать эмпирические методы, основанные на анализе высоких (или низкий) процентили распределения вероятностей интересующей переменной. Фактически, обычно предполагается, что теория слишком требовательна к данным, чтобы ее можно было эффективно применять в большинстве доступных климатических временных рядов (IPCC 2012).Тем не менее, недавно было показано, что теория экстремальных значений может строго и надежно применяться также в случае относительно коротких временных рядов в несколько десятков лет, см., Например, Захид и др. (2017).
Мы упомянули выше проблему постоянства. В целом устойчивые события можно анализировать двумя способами: во-первых, рассматривая их как совокупность последовательных экстремальных событий и изучая свойства групп экстремальных явлений (Ферро и Сегерс, 2003 г., Сегерс, 2005 г.), или, во-вторых, рассматривая PDF-файлы времени. -средние наблюдаемые.В этом исследовании мы следуем второму маршруту. Следуя интуиции, если мы посмотрим на PDF средних конечных размеров наблюдаемого, можно ожидать, что хвосты распределения в основном заполнены средними значениями, происходящими из устойчивых крайностей. Обоснованием этого является то, что окно усреднения действует как фильтр нижних частот на длине рассматриваемых постоянных событий, приводя к связи между крайними значениями средних значений и постоянными событиями с определенной длиной (большей или приблизительно равной выбранному окну усреднения. ).Фактически, это будет примерно тот сценарий, который мы рассмотрим ниже. Однако связь между устойчивостью и крайними значениями средних конечных размеров не всегда верна: например, в случае случайных величин с тяжелыми хвостами в крайних значениях средних значений преобладает одно очень большое экстремальное событие в пределах окна усреднения (Mikosch и Нагаев 1998). Отметим, что, как правило, методы теории экстремальных значений также могут применяться таким же образом для изучения экстремумов усредненных наблюдаемых. Однако процесс усреднения уменьшает объем доступных данных, поэтому применение этих методов может стать более трудным по мере увеличения длины окна усреднения.
1.1.2. Теория больших отклонений.
Мощная математическая структура, описывающая свойства PDF усредненных наблюдаемых, обеспечивается теорией больших отклонений (LDT), введенной Крамером (1938) и далее развитой другими математиками, такими как Донскер и Варадхан (1975a, 1975b, 1976, 1983) , Гертнер (1977) и Эллис (1984). Центральный результат теории состоит в записи вероятности усредненных случайных величин: поскольку вероятность усреднения убывает экспоненциально с n ,.Это называется принципом большого отклонения . Скорость распада описывается так называемой функцией скорости. Вероятность p ( A n = a ) везде убывает с увеличением n , кроме случаев. Здесь, . Для независимых одинаково распределенных случайных величин, можно было бы иметь, что, где * таково, что I ( a * ) = 0. Если функция скорости существует, можно оценить вероятность средних значений для каждые n .Подобно теории экстремальных значений, если применяется предельный закон, мы получаем предсказательную силу с той разницей, что в этом случае она направлена на средние значения с увеличением n . Это означает, что больше не нужно иметь дело с проблемой уменьшения объема данных по мере увеличения n . Теория больших отклонений очень широко используется в физике, в основном в контексте термодинамики и статистической механики; см. обзор Touchette (2009).
Хотя в последнее время они применялись в контексте геофизических потоков (см. E.грамм. Bouchet and Venaille (2012), Bouchet и др. (2014) и Herbert (2015)), методы LDT до сих пор нерегулярно использовались в исследованиях климата, несмотря на то, что они могут быть полезны всякий раз, когда связь между макроскопическими и долгосрочными -срочные наблюдаемые и микроскопические или мгновенные наблюдения важны, и каждый интересуется постоянными и / или продолжительными колебаниями климатического поля.
Одна из областей моделирования климата, в которой методы, основанные на больших отклонениях, только начинают применяться, — это выборка редких явлений.Методы вычисления редких событий, основанные на элементах LDT, были разработаны с целью получения надежной статистики конкретных редких событий данной модели в качестве альтернативы длительному прямому численному моделированию (Giardina и др. 2016, Wouters and Bouchet 2016, Lestang и др. 2018). Ragone и др. (2017) описывает, как можно выбрать модельные траектории на основе алгоритма редких событий, поддерживая ансамблевую реализацию системы в состояниях, которые предпочтительно близки к состояниям, приводящим к тепловым волнам.Следовательно, можно экспоненциально передискретизировать события со сверхдлинными периодами повторяемости и, таким образом, построить более богатую статистику волн тепла, чем можно было бы получить с помощью стандартных методов Монте-Карло. Описанный метод также дает возможность исследовать динамические свойства состояния системы (такие как глобальная циркуляция и положение струйного течения), поддерживающие возникновение изучаемых экстремумов (тепловых волн).
1.2. Эта статья
В этой работе мы применяем LDT для анализа свойств устойчивых во времени и / или в пространстве экстремальных значений температуры поверхности — волн тепла или холода, — генерируемых посредством моделирования, выполненного с помощью портативной университетской модели атмосферы (PUMA) (Lunkeit et al al 1998, Fraedrich et al 2005b).Мы исследуем средние температуры, вычисленные во времени и / или в пространстве, при этом пространственное усреднение выполняется вдоль зонального направления по причинам симметрии. Мы отмечаем, что это первое исследование по анализу устойчивых климатических явлений, основанное на этом простом применении LDT. Мы выполняем моделирование неравновесных стационарных моделей с использованием идеализированных условий, которые не могут быть напрямую связаны с реалистичными состояниями атмосферы. Таким образом, целью данной работы является проверка представленной методологии и понимание возможного потенциала путем применения этих методов статистической механики к атмосфере, а не анализа реальных атмосферных условий.Однако эту работу следует также рассматривать как первый шаг в направлении применения LDT для более реалистичного моделирования климата и данных наблюдений. На этом этапе мы не исследуем динамические процессы, приводящие к волнам тепла и холода, а скорее пытаемся построить их асимптотические статистические свойства.
PUMA — подробности приведены в разделе 3 — описывает с хорошим уровнем точности динамику трехмерной атмосферы как неравновесную систему с принудительной диссипацией.Мы анализируем свойства установившегося состояния, достигаемого в результате не зависящего от времени воздействия после того, как переходная динамика была отброшена. Для широкого диапазона значений параметров PUMA поддерживает многомерную хаотическую динамику (De Cruz et al 2018). При рассмотрении связи между усредненными значениями и постоянными событиями в подходящих масштабах (как объяснено выше) большие отклонения температуры могут быть связаны с постоянными экстремальными температурными явлениями, то есть волнами тепла или периодами холода.
Следуя приведенному выше обсуждению феноменологии синоптических возмущений, мы ожидаем найти связь между пространственно протяженными и устойчивыми во времени событиями. Чтобы добиться большого отклонения при рассмотрении пространственных средних значений в турбулентной системе, нам необходимо наличие пространственно протяженной структуры длиной, скажем, L . В системе, обладающей характерным масштабом скорости U , ожидается, что такая структура сохранится в течение типичного времени порядка.В этой работе мы исследуем связь между временными и пространственными большими отклонениями, а также анализируем пространственно-временные большие отклонения. Ищем ответы на два основных вопроса:
1.
Насколько хорошо LDT описывает устойчивые в пространстве и / или во времени колебания температуры в PUMA?
2.
Какая связь между временными, пространственными и пространственно-временными большими отклонениями?
Эти вопросы потенциально актуальны, потому что, если мы найдем экспериментальные доказательства того, что предел большого отклонения действительно выполняется в случае нашего численного моделирования, есть хороший шанс вычислить вероятность возникновения произвольно длинных по времени и / или распространены в космосе (в пределах, допускаемых геометрией Земли, как будет показано ниже), тепловые волны и периоды холода.Мы отмечаем, что возможность установления законов больших отклонений в геофизических системах является нетривиальным вопросом из-за наличия временных и пространственных корреляций в нескольких масштабах. Сила этих корреляций имеет решающее значение для практического применения теории при ограниченном количестве данных. Отметим, что при рассмотрении совместной динамики атмосферы и океана поиск законов больших отклонений может стать сложной задачей. Изучая динамические индикаторы, Де Круз и др. (2018) не смогли обнаружить законы больших отклонений в случае показателей Ляпунова с конечным временем в квазигеострофической связанной модели океан-атмосфера.Ванницем и Лукарини (2016) проанализировали большие отклонения показателей Ляпунова с конечным временем, а также в низкоуровневой версии вышеупомянутой связанной модели, и обнаружили принцип больших отклонений только в случае ненулевых показателей Ляпунова, тогда как сходимость была значительно медленнее или даже отсутствовала в случае почти нулевых показателей Ляпунова.
Наша модель не показывает наличия медленных океанических масштабов времени и, следовательно, обеспечивает более простую настройку для проверки наших идей.В случае, если мы обнаруживаем связь между временными и пространственными большими отклонениями, мы можем вывести вероятность пространственных (или пространственно-временных) средних значений из одной из временных средних и наоборот. Это может быть очень полезно в случае приложений, когда, например, доступны только временные или только пространственные ряды. Чтобы проверить качество прогнозов времени возврата на основе LDT, мы сравниваем результаты с результатами, которые можно получить с помощью теории экстремальных значений (мы используем метод максимального превышения порога).
Структура статьи следующая. В разделе 2 мы приводим теоретическую формулировку LDT и некоторые элементы теории экстремальных значений. В разделе 3 мы даем описание модели PUMA и приводим детали численного моделирования, выполненного в рамках данной статьи. Мы представляем наши результаты в разделе 4. Здесь мы сначала сосредотачиваемся на связи между временными и пространственными большими отклонениями, а затем мы дополнительно рассматриваем случай пространственно-временных больших отклонений. Мы проверяем правильность и применимость наших результатов, вычисляя периоды повторяемости экстремальных значений средних температур и сравнивая их с эмпирическими данными и с периодами повторяемости, полученными на основе метода пика над порогом.Кроме того, чтобы оценить надежность и применимость предлагаемого подхода, мы проверяем, как меняются наши выводы, касающиеся периодов повторяемости, при рассмотрении более коротких временных рядов для оценки функций скорости больших отклонений. Раздел 5 завершает статью, содержащую резюме и обсуждение наших результатов и идей для будущих исследований.
2.1. Построение функций скорости, описывающих большие отклонения
Теоретическая основа больших отклонений может быть сформулирована на трех различных уровнях, соответствующих сложности статистического описания динамической системы.Они, как описано Ооно (1989), основаны на: выборочных средних наблюдаемых (уровень-1), распределениях вероятностей в пространстве состояний наблюдаемых (уровень-2) и распределениях вероятностей в пространстве пути или истории, т. Е. полный набор возможных орбит или историй системы (уровень-3). Приведенное ниже описание следует подходу уровня 1 в соответствии с научной целью данной статьи и в основном основано на работах Touchette (2009) и Oono (1989). Мы не преследуем здесь строгую математическую формулировку; наша цель, скорее, состоит в том, чтобы резюмировать основные концепции и результаты, а также ввести наши обозначения.
Мы говорим, что случайная величина, где X i являются одинаково распределенными случайными величинами, удовлетворяет принципу большого отклонения, если предел
существуют. Плотность вероятности p ( A n = a ) экспоненциально убывает с n для каждого значения a , кроме тех, для которых, где, и. — это так называемая функция скорости, представляющая скорость этого экспоненциального убывания вероятностей.Когда предел (1) выполняется и имеет уникальный глобальный минимум, A n сходится по вероятности к своему среднему значению a * и подчиняется закону больших чисел. Если тогда дополнительно является квадратичным (т.е. дважды дифференцируемым) около a * , центральная предельная теорема выполняется, что означает, что небольшие колебания вокруг среднего обычно распределены. Выражение «небольшие колебания» здесь очень важно, потому что большие колебания вокруг среднего значения не обязательно имеют нормальное распределение.Поскольку функция скорости описывает как малые, так и большие отклонения, LDT можно рассматривать как обобщение центральной предельной теоремы.
Теперь давайте рассмотрим вместо случайных величин наблюдаемые, производимые детерминированной динамической системой. Если система является аксиомой A, все ее наблюдаемые подчиняются принципу большого отклонения (Eckmann and Ruelle 1985). Если мы рассмотрим многомерную хаотическую систему, используя гипотезу хаоса, введенную Галлавотти и Коэном (1995), можно ожидать обнаружения законов больших отклонений даже в системах, которые не являются Аксиомой А.
Динамический характер неравновесных стационарных систем требует, однако, небольшой модификации нашего теоретического подхода, который в основном подразумевает, что при формулировке принципа большого отклонения необходимо учитывать время, заменяя параметр n . Из-за временных корреляций в этих системах для вычисления функции скорости требуется теория уровня 2 или уровня 3. Это было сделано для цепей Маркова и случайных величин с определенной формой зависимости и включает в основном вычисление матриц перехода или совместных PDF (den Hollander 2000, Touchette 2009).В случае немарковских процессов и многомерных систем вычисление аналитических функций скорости является безнадежным занятием. Таким образом, в этой работе мы применяем другую (очень простую) стратегию для работы с временными корреляциями. В случае слабо коррелированных наблюдаемых (например, X j и X l имеют экспоненциально убывающую корреляцию, если она достаточно велика), можно воспользоваться тем фактом, что для достаточно больших n средние A n становятся практически некоррелированными.Это представляет собой основу для метода усреднения блоков (Rohwer et al 2015). Преобразуем переменные X i в переменные, где b представляет размер блока усреднения, т.е. b = n / k с количеством блоков k . В случае, когда Y i почти независимы и одинаково распределены (эргодическая цепь Маркова), принцип больших отклонений может быть получен для:
Интуитивно можно утверждать, что b должно быть как минимум настолько большим, чтобы X i и X i + b почти не коррелировали, т.е.е. где — показатель устойчивости, выраженный в количестве последовательных коррелированных данных. Обычно настойчивость количественно оценивается с помощью функции автокорреляции. Учитывая нашу научную цель — изучение вероятностей средних значений, имеет смысл выбрать интегрированную автокорреляцию в качестве общей меры устойчивости во времени и пространстве, поскольку эта величина играет центральную роль в центральной предельной теореме для цепей Маркова. , как описано ниже.
Согласно формулировке центральной предельной теоремы в случае зависимых переменных, основанной на Биллингсли (1995), предположим, что это стационарная цепь Маркова с соответствующими условиями смешивания и удовлетворяет им, тогда дисперсия выборочного среднего A n есть
где — автокорреляция, а обозначает автоковариацию при лаге k ,.Уравнение (3) показывает, что измененная дисперсия выборочного среднего значения цепи Маркова сходится к дисперсии, умноженной на X 1 раз интегрированной автокорреляции.
Хорошо известно, что центральная предельная теорема нарушается, когда большие экстремальные значения доминируют над колебаниями около среднего. В этих случаях вероятность сумм сходится к более общему пределу вместо гауссова распределения. Этот предел представлен классом безгранично делимых распределений, включая альфа-стабильные распределения Леви (West et al 2003).Как следствие расходящихся вторых (или даже первых) моментов распределения стохастической переменной ссылки, вероятность сумм убывает субэкспоненциально, а функция скорости тривиально равна 0 (Touchette 2009). Во многих случаях все же можно получить результаты с большим отклонением; однако в них преобладают самые большие значения в выборке, а не среднее, как уже упоминалось во введении (Mikosch and Nagaev 1998). Эти условия актуальны для некоторых переменных, представляющих интерес в (ге) физической гидродинамике.Показано, что для некоторых переменных турбулентных течений центральная предельная теорема не выполняется. Например, разности скоростей (или градиенты) между двумя точками в пространстве часто имеют длинные хвосты как эффект долгоживущих сильных вихрей вблизи диссипативного диапазона масштабов (Biferale 1993, Jiménez 1996, Jiménez 2000). Также было обнаружено, что некоторые климатические переменные демонстрируют возрастающую изменчивость на низких частотах: атмосферные поверхностные переменные в тропиках (из-за эффекта импульсных конвективных явлений) или температура морской поверхности в некоторых регионах (Blender et al 2008, p. Fraedrich et al 2009).Ожидается, что в этих случаях долговременная память препятствует сходимости к тому, что было предсказано центральной предельной теоремой, по крайней мере, в соответствующих конечных масштабах.
2.2. Теория экстремальных значений: подход «пик над порогом»
Простой способ исследовать экстремальные значения усредненных величин, очевидно, заключается в использовании теории экстремальных значений. Обратите внимание, что, несмотря на то, что такой подход неосуществим или непрактичен во многих практических приложениях, поскольку процедура усреднения резко уменьшает размер набора данных, наше численное моделирование достаточно длительное, чтобы обеспечить надежную реализацию также в случае средних значений.Ниже мы кратко резюмируем основные идеи теории экстремальных ценностей.
Рассмотрим, где — последовательность независимых и одинаково распределенных случайных величин с общей функцией распределения. Теорема Фишера – Типетта – Гнеденко (Фишер и Типпет, 1928, Гнеденко, 1943) утверждает, что распределение правильно нормированных максимумов блоков Z м сходится при определенных условиях к так называемому обобщенному распределению экстремальных значений, с тремя параметрами: параметром местоположения, параметром масштаба и параметром формы:
где, для и для (Coles 2001).
Пикандс (1975) переформулировал теорему Фишера – Типетта – Гнеденко на основе условной вероятности значений, превышающих высокий порог u и достигающих верхней правой точки распределений X , при условии, что X > u. . В тех же условиях, когда распределение Z м сходится к обобщенному распределению экстремальных значений, превышения y = X — и асимптотически распределяются в соответствии с обобщенным семейством распределений Парето (Coles 2001)
где при, y > 0, и.имеет два параметра: параметр масштаба и параметр формы. Параметр формы описывает спад вероятностей в хвосте распределения и определяет, к какому из трех возможных типов обобщенных распределений Парето принадлежит. Если, распад хвоста экспоненциальный; если, распад хвоста полиномиален; и если распределение ограничено, т.е. крайности ограничены сверху (Balkema and de Haan 1974, Pickands 1975). Параметры обобщенного экстремального значения и обобщенного распределения Парето связаны следующим образом: и (Coles 2001).Это означает, что два подхода (блочные максимумы и пик над порогом) для исследования экстремумов асимптотически эквивалентны.
Классическая теория экстремальных значений была расширена для работы со слабо коррелированными случайными величинами (Leadbetter и др. , 1983) и адаптирована для анализа крайних значений наблюдаемых хаотических динамических систем. Подробный обзор этой области исследований предоставлен Лукарини и др. (2016), где показано, что, если рассматривать систему аксиомы А, можно получить, что экстремальные значения различных классов наблюдаемых могут использоваться для вывода свойств устойчивого и неустойчивого многообразия, включая возможность оценки размерности Каплана – Йорка (Eckmann, Ruelle, 1985).Так же, как обсуждалось выше, принимая гипотезу хаоса (Gallavotti and Cohen 1995), можно ожидать, что такие открытия применимы к более общим системам, обладающим многомерным хаосом; см. подробный анализ в Bódai (2017) и точное исследование в случае многомерной системы (с O (10 3 ) степеней свободы) в Gálfi et al (2017). Теория экстремальных значений в сочетании с анализом повторяемости оказалась очень полезной для обеспечения новой основы для определения так называемых погодных режимов в реальных климатических данных и в выходных данных климатических моделей, а также для интерпретации их конкретных динамических свойств (Faranda et al. 2017, Мессори и др. 2017).
2.3. Периоды повторяемости и уровни доходности
Мы сравниваем два метода анализа редких событий на практическом уровне, то есть на основе периодов повторяемости и уровней доходности. В случае LDT мы оцениваем периоды повторяемости – событий, превышающих значение –, используя общую формулу, где представляет собой кумулятивную функцию распределения закона больших отклонений согласно данным. В случае подхода «пик над порогом» ожидаемые уровни доходности могут быть явно записаны в терминах обобщенных параметров Парето, которые могут быть выведены с помощью обычных проверенных методов оценки, таких как оценка максимального правдоподобия (Coles 2001) или L-моменты ( Хоскинг 1990 г.).Уровень y r , который превышается в среднем один раз каждые r наблюдений, называется уровнем доходности наблюдений r и является решением проблемы. Из этого следует, и, следовательно, (Coles 2001):
В результате последовательных корреляций превышения пороговых значений могут быть организованы в кластеры. Если в этом случае вообще существует закон экстремального значения, необходимо ввести так называемый экстремальный индекс — инверсию предельного среднего размера кластера — который необходимо учитывать при оценке обобщенных параметров Парето с за исключением параметра формы (Coles 2001).Широко применяемый метод борьбы с коррелированными превышениями пороговых значений — это применение декластеризации, которая в основном направлена на определение максимального превышения в каждом кластере, а затем на согласование обобщенного распределения Парето с максимумами кластера (Leadbetter и др. 1989, Ferro and Segers 2003 ). Здесь, поскольку операция усреднения резко снижает эффект последовательной корреляции, подход пика над порогом может быть применен прямым способом, аналогично случаю независимых и одинаково распределенных случайных величин.
Мы выполняем моделирование с помощью PUMA, которая представляет собой упрощенную спектральную модель общей циркуляции, разработанную в Гамбургском университете. PUMA использовалась для исследования нескольких атмосферных явлений, таких как динамика штормовых траекторий или низкочастотная изменчивость (Lunkeit et al 1998, Fraedrich et al 2005b), и даже была адаптирована для внеземных атмосфер (Grieger et al 2004). В недавнем исследовании изучаются свойства спектра Ляпунова в PUMA, включая большие отклонения показателей Ляпунова с конечным временем (De Cruz et al 2018).PUMA — это сухое ядро Planet Simulator (PlaSim), модели климата средней сложности (Fraedrich и др. 2005a, Lucarini и др. 2010).
Далее мы резюмируем уравнения модели и применяемые параметризации. Более подробное описание модели можно найти в (Fraedrich et al 2009). Как это обычно делается при атмосферном моделировании, физика модели в основном описывается примитивными уравнениями для атмосферы, которые представляют собой модификацию уравнения Навье – Стокса во вращающейся системе отсчета, где вертикальное ускорение жидкости ограничено величиной быть маленьким по сравнению с гравитацией (Klein 2010).Эти уравнения дают хорошее представление о динамике атмосферы для горизонтальных пространственных масштабов, превышающих несколько десятков км (Holton 2004). По сравнению с полной моделью общей циркуляции атмосферы, влажные процессы не учитываются, и используются простые параметризации для учета эффекта трения (трение Рэлея), диабатического нагрева (ньютоновское охлаждение) и диффузии. Члены ньютоновского охлаждения и трения Рэлея такие же, как предложенные Хелдом и Суаресом (1994) для сравнения динамических ядер моделей общей циркуляции.Уравнения модели учитывают сохранение импульса, массы и энергии. Прогностические уравнения для абсолютной завихренности, заданные суммой относительной завихренности ζ и планетарной завихренности f , горизонтальной дивергенции скорости D , температуры T и давления на поверхности p s можно записать, используя сферические координаты и вертикальную систему, следующим образом:
с участием
Переменные и параметры, используемые в уравнениях (7) — (10), перечислены в таблице 1.
Таблица 1. Список переменных и параметров в PUMA, уравнения (7) — (10).
Горизонтальное представление переменных прогностической модели дается серией сферических гармоник, которые интегрируются во времени с помощью полунеявной схемы дифференцирования во времени (Хоскинс и Саймонс, 1975). Линейные вклады в прогностических уравнениях вычисляются в спектральном пространстве, нелинейные вклады в пространстве точек сетки. Горизонтальное разрешение определяется треугольным усечением.Вертикальная дискретизация основана на конечных разностях на равноотстоящих уровнях. Вертикальная скорость установлена на 0 на верхней () и нижней () границах.
Рэлеевское демпфирование горизонтальных скоростей с временной шкалой учитывает эффект трения пограничного слоя на самых низких уровнях. d at (ближайший к поверхности вертикальный уровень) и d at. Для более высоких уровней трение не учитывается, т.е. Влияние неразрешенных процессов на каскад энергии и энстрофии представлено гипердиффузией (~).Коэффициент гипердиффузии K таков, что он обеспечивает максимальное затухание самых коротких волн и не влияет на среднее состояние (волновое число 0). Целочисленный показатель степени h = 4 приводит к дополнительному затуханию коротких волн. Масштаб времени диффузии для самой короткой волны составляет 1/4 дня. Диабатический нагрев (охлаждение) параметризуется ньютоновским термином охлаждения. Это вызывает релаксацию модельной температуры к так называемому радиационно-конвективному состоянию равновесия , определяемому температурой восстановления, которая зависит только от вертикального уровня и широты.
описывает меридиональную форму температуры восстановления, тогда как учитывает вертикальные изменения в этом меридиональном профиле:
где — разница температур между северным и южным полюсами, а — разница температур между экватором и полюсом. Меридиональный градиент температуры уменьшается с высотой в тропосфере для, и исчезает в тропопаузе, для, где — высота тропопаузы. описывает вертикальный профиль температуры восстановления:
с: температура восстановления на поверхности, К; влажный адиабатический градиент, л = 6.5 тыс. Км −1 ; глобальная постоянная высота тропопаузы, км; геометрическая высота з . S позволяет сглаживать температурный профиль в тропопаузе. В случае десяти вертикальных уровней l шкала времени ньютоновского охлаждения составляет 2,5 дня на самом низком уровне при l = 10 и 7,5 дня при l = 9. продолжает монотонно увеличиваться с высотой до тех пор, пока три верхних уровня, где он установлен на 30 d.
Мы запускаем модель в простой симметричной обстановке (обычно называемой аква-планетой), т.е.е. без орографии. Мы удаляем годовой и суточный цикл и используем симметричное воздействие относительно экватора,. Мы устанавливаем разность температур между экватором и полюсом равной 90 K, создавая бароклинически более нестабильное состояние атмосферы, чем при стандартной настройке с K. Мы запускаем модель с постоянным воздействием во времени с шагом по времени 30 мин. Горизонтальное разрешение составляет T 42 (треугольное усечение спектра с 42 зональными волнами), а вертикальное разрешение состоит из десяти уровней.Продолжительность моделирования составляет 10 4 лет, за исключением переходного периода в 5 лет, которые отбрасываются для учета условий устойчивого состояния. Мы рассматриваем для нашего анализа температуру воздуха на самом нижнем вертикальном уровне на уровне 960 гПа при суточной производительности. Переменная спектральной температуры преобразуется во время постобработки в пространство точек сетки, состоящее из эквидистантной сетки широты и долготы.
Используя те же настройки модели, что и выше, но с более низкой разностью температур между экватором и полюсом, Де Круз и др. (2018) оценили размерность Каплана – Йорка, равную 187, и ряд положительных показателей Ляпунова равным 68 для K. .В этом исследовании K, таким образом, модельная атмосфера бароклинно значительно более нестабильна, чем в упомянутом исследовании. Таким образом, для грубой оценки количество положительных показателей Ляпунова> 80 в нашей системе. Следовательно, мы ожидаем от этой установки хаоса очень большой размерности, который удовлетворяет хаотической гипотезе, о чем также свидетельствует быстрое затухание автокорреляций на рисунках 2 (c) и (d) ниже. В результате мы ожидаем, что результаты нашей модели могут быть проанализированы с использованием теории экстремальных значений и LDT, как обсуждалось выше.Тем не менее, a priori неясно, можно ли четко определить асимптотический результат при конечном размере, учитывая длину наших численных интегрирований. Обратите внимание, что в De Cruz et al (2018) было показано, что показатели Ляпунова с конечным временем подчиняются закону больших уклонений.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 2. Общие свойства температурного поля при 960 гПа.(a) Значения температуры T ( x , y , t * ) как функция долготы x и широты y в один выбранный момент времени t * . (b) Значения температуры T ( x * , y , t ) как функция широты y и времени t на одной выбранной долготе x * ( x — ось назад во времени).(c) Временная и (d) зональная автокорреляционная функция согласно (16) и (17) для выбранных широт (разные цвета согласно легенде). (д) Вариация приповерхностной температуры согласно (15). Пунктирными линиями на (a), (b) и (e) отмечены выбранные широты.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияПрежде чем обсуждать наши основные результаты, связанные с большими отклонениями температуры, полезно иметь общую картину свойств моделируемого температурного поля при 960 гПа (т.е.е. близко к поверхности). Для анализа временных, зональных и пространственно-временных больших отклонений мы выбираем три широты: 60 °, 46 ° и 30 °. Мы сосредотачиваемся на средних широтах, потому что это область атмосферы с самой сильной турбулентностью, поэтому мы ожидаем, что соответствующие наблюдаемые должны вести себя в соответствии с хаотической гипотезой; см. обсуждение в Gálfi et al (2017). Мы отмечаем, что включение влажных процессов, более полных параметризаций и менее идеализированных граничных условий значительно увеличило бы хаотические процессы, а более высокое разрешение по горизонтали и вертикали привело бы к значительно более сильной турбулентности в тропическом поясе.
В рассматриваемой ситуации два полушария имеют идентичные статистические свойства; Кроме того, два полушария слабо связаны, в основном, в результате выбранных граничных условий, отсутствия сезонного цикла и закона сохранения потенциальной завихренности. Следовательно, мы можем рассматривать временные ряды, исходящие из двух полушарий, как отдельные реализации одного и того же динамического процесса. Далее мы сначала проводим качественное сравнение временных и пространственных характеристик температурного поля, а затем количественно определяем устойчивость во времени и пространстве на основе интегрированной автокорреляции.Мы отмечаем, что мы проводим анализ в рамках Эйлера, соответствующего нашей цели изучения стойких экстремальных температур с пространственно фиксированной точки зрения: это дает наиболее актуальную информацию для конкретной проблемы — исследования стойких температурных аномалий — у нас есть в уме.
Рисунок 2 (a) иллюстрирует температурное поле T ( x , y , t * ) как функцию долготы x и широты y в один выбранный момент времени t * , тогда как на рисунке 2 (b) представлено температурное поле T ( x * , y , t ) как функция широты y и времени t за один выбранная долгота x * .Качественно аналогичные цифры будут получены для различных значений т * и x * соответственно. Обратите внимание, что для облегчения сравнения между пространством и временем ось x на рисунке 2 (b) направлена назад во времени согласно преобладающим восточным зональным ветрам (также называемым западными ветрами) в средних широтах (Holton 2004). Кроме того, диапазон оси x на рисунке 2 (b) такой же, как на рисунке 2 (a), после того как мы изменим масштаб оси времени в соответствии с масштабной скоростью, представленной ниже (вычисленной для 46 °), которая взвешивает распад корреляции в пространстве в фиксированное время и во времени в фиксированном месте.Сравнивая эти две фигуры, мы понимаем, что, разрезая по времени или по долготе, мы получаем очень похожие волнистые узоры, что неудивительно, поскольку воздействие инвариантно во времени и вдоль широтной полосы.
Хотя этот результат был бы тривиальным при наблюдении периодического или квазипериодического сигнала, мы должны учитывать здесь, что динамика атмосферы представляет собой нетривиальную смесь волн, турбулентности и частиц (Ghil and Roberston 2002), поэтому что нам нужно взглянуть на это пространственно-временное подобие со статистической точки зрения.В соответствии с этим мы имеем, что на заданной широте y * временной ряд и зональный ряд выбираются из двух одинаково распределенных случайных процессов при условии устойчивого состояния и дискретной симметрии по отношению к перемещению вдоль широты.
Основное различие между и связано с отдельными масштабами временных и пространственных характеристик, то есть с временными или пространственными корреляциями. В средних широтах циклоны имеют типичный временной масштаб 1 день и характерный пространственный масштаб около 1000 км (Holton 2004).Очевидно, что эти шкалы важны, когда мы пытаемся получить принцип больших отклонений, поэтому очень важно найти адекватную метрику для их описания.
Мы количественно оцениваем типичные временные и зональные масштабы на основе интегрированной автокорреляции, как объяснено в разделе 2. Мы вычисляем автокорреляции временных и зональных рядов на выбранной широте y * , на основе которых позже мы получим интегрированные временные и зональные автокорреляции. Для этого мы используем 1000 лет нашего моделирования из 10 000 лет, поскольку этого более чем достаточно для получения надежных оценок.Как описано в разделе 2, автокорреляция определяется как соотношение между автоковариацией при лаге l и дисперсией:. Чтобы получить более точные оценки автокорреляции, мы вычисляем пространственно-временное среднее и дисперсию для каждых y * и используем эти оценки для вычисления временных и зональных автокорреляций:
а также
где — количество рассматриваемых точек во времени (дневные данные), а N x = 128 — количество точек сетки в зональном направлении.Это разумно, учитывая симметрии в нашей системе во времени и по широтным окружностям. Индексы t и x относятся ко времени и к зональному измерению, также и далее.
В случае временного ряда мы вычисляем автоковариацию на одной выбранной долготе x * . Эта оценка не зависит от x * , поэтому неважно, какую долготу мы выберем. У нас есть:
Однако длина зонального ряда слишком мала для получения надежных оценок автокорреляции.Число точек сетки вдоль зонального измерения составляет всего 128. Наряду с таким ограничением, связанным с размером Земли , существует еще одно, связанное с формой Земли . Фактически, мы должны уменьшить максимальное отставание до N x /2 = 64, потому что при больших задержках корреляции снова начинают увеличиваться из-за периодичности вдоль широтного круга. Чтобы повысить надежность нашей оценки, мы сначала вычисляем коэффициенты зональной автокорреляции с запаздыванием в каждый момент времени, а затем берем среднее значение по времени:
На рисунке 2 (c) показан коэффициент временной автокорреляции как функция временного запаздывания в днях, тогда как на рисунке 2 (d) показан коэффициент зональной автокорреляции как функция пространственного запаздывания, выраженного в виде долготных индексов. i x = 0,1,2,…. Как временные, так и пространственные автокорреляции уменьшаются до нуля, что означает, что два значения температуры, которые находятся далеко друг от друга во времени или пространстве, независимы для всех практических целей. Наконец, мы оцениваем интегрированные временные и зональные автокорреляции, суммируя коэффициенты автокорреляции до максимального запаздывания. Обратите внимание, что мы используем одинаковые временные и зональные максимальные запаздывания для согласованности. Временная интегрированная автокорреляция может быть получена также для больших максимальных задержек, но это изменяет оценочное значение лишь незначительно, поскольку спад до 0 происходит относительно быстро.Мы определяем:
составляет 1,32 при 60 °, 1,05 при 46 ° и 1,61 при 30 ° (в единицах временных шагов, которые эквивалентны дням), тогда как составляет 3,26 при 60 °, 3,54 при 46 ° и 7,68 при 30 ° (в единицах узлов сетки, которые соответствуют 391 км под углом 60 °, 732 км под углом 46 ° и 1292 км под углом 30 °). Мы определяем и в безразмерной форме (то есть как количество единиц времени или зональных точек данных), чтобы облегчить сравнение временной и пространственной устойчивости на основе разрешения наших данных, и поскольку в этой форме мы можем использовать их непосредственно для масштабирование функции скорости, как показано ниже.
Мы определяем масштабную скорость, где — временной шаг, равный 1 дню, а — шаг сетки, зависящий от широты. Со статистической точки зрения, это соотношение между пространственной и временной устойчивостью 6 . С геометрической / динамической точки зрения представляет собой соотношение типичных пространственных и временных масштабов. Таким образом, это мера анизотропии между пространством и временем. При 60 ° мс -1 и 46 ° мс -1 . Для этих широт масштабная скорость хорошо согласуется со средней зональной скоростью на 960 гПа, которая равна 3.6 мс −1 при 60 ° и 6 мс −1 при 46 °. В этом нет ничего удивительного, поскольку в первом приближении турбулентные структуры переносятся средним потоком.
Согласие теряется при взгляде на 30 °, границу бароклинной зоны средних широт, к которой применимо приведенное выше качественное описание. По мере приближения к экватору динамика атмосферы имеет гораздо меньшую степень хаотичности по сравнению со средними широтами, если мы не посмотрим на конвективные масштабы, которые вообще не разрешены в этой модели.Пространственная устойчивость сильно усиливается (см. Также рисунки 2 (а) и (b) в результате преобладания более крупных структур, связанных с нисходящим потоком ячейки Хэдли, а не синоптических возмущений, связанных с погодными системами средних широт, перенесенными преобладают западные ветры. В этом случае мы находим мс −1 , тогда как −3,4 мс −1 , что указывает на преобладающий восточный поток, явный признак тропической динамики.
Рисунок 2 (e) подчеркивает, что приповерхностный Наибольшие отклонения температуры наблюдаются в районе 46 ° широты в результате очень сильной бароклинной нестабильности, связанной с погодными условиями в средних широтах.Эта широта также соответствует среднему положению струи, локализованной области, где скорость верхних ветров максимальна (Holton 2004).
Прежде чем продолжить описание больших отклонений во времени и пространстве, мы кратко обсудим связь между высокими значениями крупнозернистых температур и длительными отдельными событиями, когда показания температуры постоянно превышают долгосрочные средние значения, обсуждаемую уже в разделе 1. На рисунках 3 (a) — (c) показаны три коротких временных ряда на широте 46 ° вместе с соответствующими рядами крупнозернистых величин, где средние значения вычисляются с использованием длин блоков, и, соответственно.Три коротких временных ряда были выбраны специально, потому что они характеризуются большим колебанием крупномасштабной величины. Рисунки 3 (d) — (f) показывают то же самое в случае зональных полей. Главный вывод заключается в том, что вплоть до умеренно длинных окон усреднения около (или для пространственных средних значений) можно связать большие флуктуации с отдельными устойчивыми событиями. Когда рассматривается более крупная зернистость, с использованием окна для средних по времени и / или для пространственных, то есть в направлении режима больших отклонений, обсуждаемого ниже, у нас нет такой однозначной идентификации.Напротив, большие сверхдлительные колебания связаны с появлением последующих умеренно длительных устойчивых особенностей.
Увеличить Уменьшить Сбросить размер изображения
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения4.1. Связь между временными и зональными большими отклонениями
На этом этапе мы обращаем наше внимание на оценку временных и зональных функций скорости.Для этого мы сначала должны получить последовательности временных и зональных средних значений для увеличения длины блоков усреднения n t и n x , для которых мы используем общую длину нашего моделирования лет. .
Длины блоков временного усреднения выбираются кратными:. Точно так же длины блоков зонального усреднения кратны, но в этом случае максимально возможное кратное м ограничено из-за размера и формы Земли, как упомянуто выше:. м = 20 в случае широты 60 ° и 46 °, тогда как м = 10 в случае широты 30 °. Чтобы увеличить количество усредненных значений для вычисления функций темпов времени, мы объединяем средние временные значения для каждой 25-й долготы вдоль широтного круга. Поскольку эти временные последовательности можно рассматривать как независимые реализации 7 . В случае зонального усреднения мы берем одно усредненное значение в пространстве из каждой десятой точки по оси времени, что мы также считаем независимыми реализациями 8 .Такое предположение является разумным, поскольку интегрированная временная автокорреляция средних зональных значений намного меньше 10, даже для наибольшего n x (как показано ниже на рисунке 5). Мы получаем для каждого значения n t и n x оценки функций скорости после использования коэффициентов повторной нормализации, задаваемых формулами или, соответственно:
где и представляют собой эмпирические оценки PDF усредненных по времени и зонам последовательностей.Из-за повторной нормализации логарифм вероятностей масштабируется на или, то есть на количество некоррелированных данных, а не на общий объем данных в блоке усреднения. Таким образом, мы исключаем влияние корреляций.
На рисунке 4 показаны (a – c) и (d – f) для каждых n t и n x . В качестве примечания отметим, что на каждом рисунке ниже показанные перенормированные оценки функции скорости сдвинуты по вертикали, так что их минимум равен 0.В случае функций темпов времени ясно, что оценки не меняют форму при дальнейшем увеличении на n t , что означает, что мы получаем стабильные и надежные оценки, т.е. данные для принципа большого отклонения во времени. Мы также замечаем, что диапазон значений сужается по мере увеличения n t в результате усреднения, что уменьшает количество доступных данных. Таким образом, мы получаем нашу наилучшую оценку при оптимальной длине блока усреднения, которая достаточно велика, чтобы обеспечить сходимость оценок функции скорости, но в то же время достаточно мала, чтобы диапазон не был слишком узким, т.е.е. . Выберем одинаковую оптимальную длину усреднения для всех трех широт:; хотя в случае широт 60 ° и 30 ° уже кажется хорошей оценкой для асимптотики. Сравнивая повторно нормализованные оценки функции скорости на выбранных широтах, мы понимаем, что функция скорости имеет меньшую кривизну на широте 46 °, чем на 60 ° и 30 °. Это нетривиальное следствие большей изменчивости системы в середине рассматриваемой области, как упомянуто выше и показано на рисунке 2 (e), потому что здесь мы рассматриваем средние значения колебаний.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 4. (a) — (c) Оценки временной перенормированной функции скорости и (d) — (f) оценки зональной перенормированной функции скорости для трех рассматриваемых широт и для увеличения продолжительности усреднения n t и n x в зависимости от цвета (см. Легенду). (g) — (i) Наилучшие оценки временной (красный) и зональной (синий) перенормированных функций скорости.Все оценки сдвинуты по вертикали, так что их минимум равен 0. Представляет колебания температуры вокруг среднего значения.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияВ случае зональных функций скорости мы сначала замечаем, что наибольшее значение n x кажется слишком маленьким для четкой сходимости. Другими словами, широтный круг недостаточно длинный, чтобы четко получить предел большого отклонения. Однако зависимость от n x , похоже, уменьшается по мере увеличения n x , поэтому мы выбираем максимально возможное значение n x в качестве оптимальной длины зонального усреднения.в случае широты 60 ° и 46 °, тогда как в случае широты 30 °, это только из-за более сильных зональных автокорреляций.
Наилучшие оценки временных и зональных перенормированных функций скорости снова показаны на рисунках 4 (g) — (i). Затенение представляет 95% доверительные интервалы 2000 непараметрических оценок обычной начальной загрузки, основанных на нормальном распределении (функции boot и boot.ci пакета boot, Davison and Hinkley (1997), Canty and Ripley (2017)).Мы это замечаем. Эквивалентность очень хорошая в случае широты 60 ° и в случае отрицательных аномалий на широтах 46 ° и 30 °. Мы также замечаем некоторые различия для положительных аномалий на широтах 46 ° и 30 °, с большими различиями на 30 °. Однако на этой более поздней широте следует учитывать, что максимально возможная длина зонального усреднения составляет, тогда как в других случаях это так. Мы предполагаем, что различия между временными и зональными перенормированными оценками функции скорости связаны с тем фактом, что она недостаточно велика для правильной оценки функции скорости.Большие значения n x необходимы для преодоления повышенной асимметрии в распределении средних зональных значений как эффекта пространственных корреляций; однако это невозможно из-за ограничений, связанных с размером и формой Земли. Эти результаты соответствуют большому значению на этой широте, определяющему анизотропию между пространством и временем. В то время как временная функция скорости может быть надежно оценена при относительно небольшом значении n t , оценка зональной функции является гораздо более сложной задачей.
Однако главное сообщение на рисунке 4 состоит в том, что временная и зональная перенормированные функции скорости кажутся равными, если вероятность средних значений масштабируется на количество некоррелированных данных в блоке усреднения, или, как объяснено выше . Другими словами, существует связь, соединяющая временные и пространственные большие отклонения или средние значения из-за существования универсальной функции I n ; универсальный в том смысле, что он представляет собой большие отклонения в обоих измерениях — времени и пространстве.
Очевидно, что, основываясь на принципе больших отклонений во времени или в пространстве, невозможно охарактеризовать устойчивые временные или пространственные события, потому что предельный закон начинает действовать в больших масштабах, где постоянство теряется и возникает универсальность. Однако можно зафиксировать устойчивые пространственно-временные события, усреднив оба измерения: пространство и время. Для этого важно, чтобы длина пространственного усреднения не была слишком маленькой, но и не слишком большой, как мы покажем ниже.
4.2. Большие пространственно-временные отклонения
Мы рассматриваем временные последовательности зонально усредненных наблюдаемых на усредненных длинах, а затем усредняем каждую последовательность во времени для увеличения усредненных длин. Обозначение означает, что мы усредняем по пространству и дополнительно по времени, и это время декорреляции пространственно усредненной наблюдаемой. Рассматривая несколько значений n x , мы выбираем пространственный масштаб, в котором мы анализируем большие отклонения во времени.Пространственно-временные средние вычисляются как:
Как и в предыдущих случаях, также в случае пространственно-временных средних, мы должны учитывать силу автокорреляций, если мы стремимся сравнивать пространственно-временные функции скорости с временными и зональными. Мы оцениваем интегрированную временную автокорреляцию пространственно-временных средних значений аналогично или, но для обеспечения стабильности мы выбираем более высокое максимальное запаздывание, равное 120 суткам, поскольку автокорреляция во времени зональных средних значений имеет более медленное затухание. по сравнению с неусредненными временными или зональными наблюдаемыми.На рисунке 5 показаны зависимости от длины зонального усреднения n x и временного усреднения. Временные автокорреляции пространственно-временных наблюдаемых увеличиваются с n x и уменьшаются с. Увеличение на n x , с одной стороны, можно объяснить связью между временными и пространственными масштабами. Как обсуждалось в разделе 1 9 , крупные события в космосе — это длительные события во времени.Уменьшение временной интегрированной автокорреляции с, с другой стороны, можно объяснить увеличением количества некоррелированных событий по отношению к количеству коррелированных событий в блоке усреднения как следствие увеличения длины блока. Это автоматически имеет место для больших блоков усреднения, когда корреляции конечны, и имеет решающее значение для применимости метода усреднения блоков. Различное поведение с n x и, однако, связано в основном с расхождениями во временном разрешении вновь полученных средних значений.В то время как в случае зонального усреднения временное разрешение остается одним днем, в случае дополнительного усреднения по времени временное разрешение уменьшается с, таким образом, временная задержка автокорреляции увеличивается. Однако это не проблема для нашего анализа, поскольку нас интересуют корреляции усредненных наблюдаемых, измеренных в количестве усредненных данных. Более сильное увеличение на «конце» канала подчеркивает описанный выше эффект усреднения по широтному кругу.В зональном «конце» канала значения температуры сильно коррелируют со значениями в «начале» канала.
Увеличить Уменьшить Сбросить размер изображения
Рис. 5. Интегрированная временная автокорреляция пространственно-временных средних для выбранных широт как функция от длин зонального и временного усреднения. Вертикальными линиями отмечены длины зонального усреднения, соответствующие кратным: (от белого к зеленому).
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияЗависимость от длин зонального и временного усреднения качественно аналогична для выбранных широт, если рассматривать n x в единицах (по вертикальным линиям на рисунке 5 с одинаковыми цветами). По мере продвижения с юга на север автокорреляции зонально усредненных наблюдаемых усиливаются. Это, однако, в основном связано с уменьшением расстояния между долготами, что приводит к более сильной коррелированности значений температуры на соседних долготах.
Затем вычисляются оценки пространственно-временных повторно нормализованных функций скорости для каждого n x и как:
Отметим, что уравнение (22) учитывает как зональные, так и временные автокорреляции путем умножения на, аналогично случаю временных и зональных функций скорости. Оценки пространственно-временной перенормированной функции скорости показаны на рисунке 6 (цветные линии). В целях сравнения мы также показываем лучшие временные и зональные оценки (сплошные черные линии) и (короткие пунктирные черные линии) вместе с оценкой зональной перенормированной функции скорости на выбранной длине зонального усреднения (длинные пунктирные черные линии). линий).Главный посыл здесь таков:
Увеличить Уменьшить Сбросить размер изображения
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияРенормализованные пространственно-временные функции скорости отличаются от универсальной функции I n в случае широт 60 ° и 46 °, а также в случае широты 60 °, хотя в этом последнем случае стоит упомянуть, что пространственно-временная функция скорости соответствует оценке зональной функции скорости в.Во всех этих случаях пространственно-временные функции скорости более плоские, чем универсальная функция, что указывает на более высокую вероятность больших отклонений, что способствует наличию организованных структур в виде устойчивых погодных условий. В самом деле, это новый способ оценки существования конкретных динамических механизмов, которые приводят к определенным статистическим свойствам температурных полей, связанных с низкочастотной изменчивостью атмосферы, обсуждаемой во введении. На рисунке 7 схематически представлены диапазоны временных и зональных длин усреднения, при которых универсальность проявляется (синий) или затруднена (голубой) из-за зональных корреляций.Белым цветом показаны предасимптотические области, в которых закон больших уклонений еще не выполняется.
Увеличить Уменьшить Сбросить размер изображения
Рис. 7. Схематическое изображение универсальности и эффекта корреляций в зависимости от длин зонального и временного усреднения. Темно-синим цветом обозначена область, в которой проявляется универсальность. Светло-голубой цвет представляет область с неуниверсальными пространственно-временными функциями скорости как эффект зональных корреляций.Предасимптотические области, т. Е. Где закон больших уклонений еще не выполняется, окрашены в белый цвет.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияВ качестве примечания, горизонтальный сдвиг оценок функции скорости при малых длинах усреднения ( n x или) на рисунке 6 подчеркивает, что эти оценки ненадежны, поскольку длина усреднения слишком мала для закона большие числа держать. Мы также хотим отметить, что различия возникают при просмотре данных о температуре с 30 ° широты.Здесь пространственно-временная перенормированная функция скорости в не идентична универсальной функции I n . Одна из возможных причин этого заключается в том, что при усреднении по длине вновь определенная наблюдаемая уже имеет свойства, значительно отличающиеся от свойств локальной (в пространстве), зависящей от времени наблюдаемой. Универсальность пространственно-временной функции скорости не может быть проверена должным образом из-за ограничения на длину зонального усреднения. Однако мы видим, что пространственно-временная перенормированная функция скорости очень похожа на универсальную функцию, но отличается от нее.
4.3. Уровни возврата больших отклонений
Мы кратко резюмируем наши основные результаты, представленные до сих пор:
1.
При рассмотрении временных средних, оценки функций скорости, кажется, сходятся к асимптотической функции, и мы получаем наилучшую оценку функции скорости при оптимальной длине блока усреднения. Мы показываем, что существует принцип больших отклонений, то есть универсальный закон, который позволяет нам оценивать вероятности появления средних значений без необходимости фактически выполнять усреднение.2.
Пространственные средние значения температурного поля вдоль широт подчиняются тому же закону больших отклонений, который получен для временных средних. Это означает, что мы можем вывести статистические свойства временных средних из пространственных средних и наоборот. Кроме того, такой же асимптотический закон получается при выполнении длинных пространственных и временных (двумерных) средних.
3.
Временные средние значения температурных полей, усредненные в промежуточных пространственных масштабах вдоль широт, подчиняются различным законам больших отклонений, которые указывают на относительно более высокую вероятность возникновения волн тепла и холода.Это свидетельствует о преимущественном существовании организованных пространственных структур, соответствующих известной низкочастотной изменчивости атмосферы.
Теперь вопрос в том, как мы можем использовать эту информацию на практике. Одно из возможных приложений, которое мы представляем в этом подразделе на примере широты 60 °, возникает в контексте вычисления периодов повторяемости крупных событий. На рисунке 8 показаны графики уровней доходности, то есть уровни доходности как функция периодов доходности, полученные тремя разными способами, на основе эмпирических данных (кружки), принципа больших отклонений (непрерывные линии) и обобщенного распределения Парето (пунктирные линии).Для оценки периодов возврата на основе предела большого отклонения мы сначала получаем оценки плотности ядра (функциональная плотность статистики пакетов, R Core Team (2016)) PDF-файлов p ( A n = a ) с фиксированными эквидистантными уровнями доходности, на основе которых мы оцениваем кумулятивную функцию распределения, а затем вычисляем периоды возврата для as и for as. Таким образом, мы получаем периоды повторяемости как положительных (рисунки 8 (a), (c) и (e)), так и отрицательных (рисунки 8 (b), (d) и (f)) больших отклонений.Затенение вокруг непрерывных линий на рисунке 8 представляет 95% доверительные интервалы для 2000 непараметрических оценок периода повторяемости обычного бутстрапа, основанных на нормальном распределении.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 8. Уровни возврата и периоды возврата положительных (верхняя строка) и отрицательных (нижняя строка), (a) — (d) временных и (e) — (f) пространственно-временных больших отклонений температуры на широте. 60 °.Маркеры кружками: эмпирические данные; непрерывная линия с затемнением: оценки, основанные на больших отклонениях с 95% доверительными интервалами 2000 непараметрических выборок начальной загрузки на основе нормального распределения; Пунктирная линия с затемнением: обобщенные оценки Парето с 95% доверительными интервалами, основанные на оценке максимального правдоподобия. Разные цвета обозначают разную длину усреднения. Оценки больших отклонений получены на основе временных средних значений (a), (b), (e) и (f) при, и (c), (d) средних зональных значений при.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияМы вычисляем обобщенные уровни доходности по Парето на основе (6) с использованием оценок максимального правдоподобия обобщенных параметров Парето (функции gpd.fit и gpd.rl пакета ismev, Stephenson (2016)). Мы анализируем уровни возврата высокотемпературных значений, превышающих пороговое значение, равное 99,9% квантиля усредненного ряда, а также уровни возврата низкотемпературных значений ниже квантиля 0,1%. Чтобы проверить применимость метода пика над порогом, стабильность уровней возврата была проверена также для более высокого (нижнего) квантиля 99.99% (0,01%). Оценки уровня доходности кажутся стабильными, даже если порог повышен (не показан). Обратите внимание, что хотя очень медленная сходимость обобщенного параметра формы Парето в некоторых случаях хорошо известна, стабильность оценок уровня доходности все еще сохраняется, если изменение параметра формы относительно невелико по мере увеличения порога (Gálfi et al 2017). . Затенение вокруг пунктирных линий на рисунке 8 представляет 95% доверительный интервал максимального правдоподобия оценок уровня доходности.В качестве примечания: в случае метода пика над порогом оценка касается уровней доходности, в то время как периоды возврата фиксированы, тогда как в случае больших отклонений мы поступаем наоборот. Это необходимо, потому что мы оцениваем функцию скорости при фиксированных эквидистантных значениях и .
На рисунках 8 (a) и (b) уровни доходности временных средних значений показаны для трех различных окон усреднения. Здесь мы используем точку 1 сверху и получаем периоды возврата на основе принципа большого отклонения для каждого окна усреднения от.Мы замечаем очень хорошее согласие с эмпирическими данными и обобщенными уровнями доходности Парето не только для, но и в случае и, как для высоких (рисунок 8 (a)), так и для низких (рисунок 8 (b)) крайних значений средних значений. В случае, доверительные интервалы для периодов наибольшей повторяемости, основанные на больших отклонениях, становятся очень нестабильными, а нижние пределы даже достигают отрицательных значений, поэтому они не могут быть отображены в этой полулогарифмической шкале.
Периоды возврата, основанные на больших отклонениях, имеют верхний (или нижний) предел, поскольку оценка основана на эмпирических PDF.Это не относится к обобщенным периодам повторяемости Парето, поскольку их можно экстраполировать даже на ненаблюдаемые события. Однако принцип большого отклонения является предельным законом, который дает нам периоды возврата для каждой длины усреднения n > n * , тогда как обобщенные периоды повторяемости по Парето должны вычисляться отдельно для каждых n . Это становится все труднее и труднее с увеличением n из-за уменьшения объема данных в результате усреднения.Другими словами, на рисунке 8 показаны различные измерения, в которых действуют два предельных закона, как уже упоминалось в разделе 1. Предсказуемость метода пика над порогом (и, в целом, предсказуемость теории экстремальных значений) направлена на все более крупные и более крупные события, т.е. в сторону ненаблюдаемых, тогда как предсказуемость LDT направлена на все большие и большие длины усреднения, то есть на наблюдаемые, которые, по своей конструкции, резко сокращают объем данных, доступных для статистического анализа.
Пункт 2, представленный выше, проиллюстрирован рисунками 8 (c) — (f). В первом случае периоды повторяемости временных средних вычисляются на основе принципа большого отклонения, полученного для зональных средних значений (), а во втором случае периоды повторяемости пространственно-временных средних (с длиной пространственного усреднения) получаются из закон больших отклонений для временных средних (). В обоих случаях, но особенно для пространственно-временных средних, согласие с эмпирическими данными и обобщенными уровнями доходности Парето хорошее.Различия между уровнями доходности, основанными на больших отклонениях и эмпирических данных (также обобщенных уровнях доходности Парето), связаны с расхождениями в оценке временных и зональных, а также временных и пространственно-временных повторно нормализованных функций ставок. Например, недооценка низких экстремумов временных средних значений на основе зональной функции скорости связана с более высокими значениями перенормированной зональной функции скорости по сравнению с временными значениями в их левом хвосте (см. Рисунок 4 (g)).Заметим, что возможность коммутировать между средними величинами различных измерений (времени и пространства) обусловлена тем фактом, что за счет устранения эффекта последовательных корреляций большие отклонения этих различных измерений следуют универсальной функции.
4.4. Насколько чувствительны наши результаты к продолжительности численного моделирования?
В типичных упражнениях по анализу данных, основанных на наборах данных наблюдений или современном климатическом моделировании, временной интервал доступных данных значительно меньше, чем в случае наших идеализированных моделей, и варьируется от до лет.Чтобы проверить применимость метода в случае более коротких временных рядов, мы разделим наши 10 000-летние модели на 100 секций по 100-летним моделям. Для каждого из них мы оцениваем уровни доходности и периоды временных средних значений на основе больших временных отклонений. Мы также оцениваем обобщенные уровни доходности по Парето, используя 95% квантиль в качестве порогового значения. После этого мы увеличиваем продолжительность моделирования и повторяем эти шаги также для 10 секций 1000-летнего моделирования. Полученные уровни и периоды доходности показаны на рисунке 9.Обратите внимание, что эмпирические уровни доходности по-прежнему получены на основе всего объема данных за 10 000 лет и, таким образом, представляют собой надежную основу для сравнения.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 9. Уровни повторяемости и периоды повторяемости положительных временных больших отклонений температуры на широте 60 °, основанные на оценках больших временных отклонений при, полученных из (а) 100-летнего и (б) 1000-летнего моделирования, а также обобщенных параметров Парето из (c) 100-летнего и (d) 1000-летнего моделирования с использованием 95% квантиля в качестве порога.Разные цвета обозначают разную длину усреднения. Круглые маркеры представляют эмпирические данные (10 000 лет), а пунктирные серые линии показывают средние оценки по повторениям.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияРисунок 9 (a) демонстрирует, что климатологически важные события с периодами повторяемости в несколько десятков и сотен лет все еще могут быть разумно аппроксимированы оценками большого отклонения, основанными на моделировании за 100 лет.Среднее значение оценок (серые пунктирные линии) немного завышает эмпирические уровни доходности; тем не менее, согласие хорошее до длительных периодов повторяемости и улучшается с увеличением продолжительности усреднения. Мы дополнительно отмечаем, что разброс прогнозов очень мал и уменьшается с увеличением длины усреднения. Это подчеркивает преимущество использования оценок больших отклонений для уровней доходности средних значений по сравнению с большими окнами усреднения и показывает, что прогнозы LDT также очень стабильны, если рассматривать гораздо более короткие наборы данных.Согласие с эмпирическими уровнями доходности существенно улучшается за счет увеличения продолжительности моделирования до 1000 лет (рисунок 9 (b)).
В случае моделирования за 100 лет обобщенные уровни доходности по Парето немного лучше согласуются с эмпирическими данными, чем оценки большого отклонения (сравните рисунки 9 (c) с (a)). Однако дисперсия обобщенных оценок Парето увеличивается сильнее с периодом повторяемости также для больших длин усреднения. Кроме того, усредненные обобщенные оценки Парето (серые пунктирные линии на рисунке 9 (c)) имеют тенденцию занижать самые крупные события как для 100-летнего, так и для 1000-летнего моделирования.Однако в случае моделирования реалистичных моделей и данных наблюдений помимо меньшего объема данных приходится иметь дело с дополнительными сложностями, в основном из-за нестационарности и сильных корреляций. Мы обсудим эти эффекты в следующем разделе.
Мы проанализировали свойства временных и пространственных средних приповерхностных (960 гПа) температур в упрощенной модели глобальной атмосферной циркуляции PUMA, основанной на LDT. Крайние значения средних значений по определенным шкалам связаны с постоянными экстремальными явлениями, такими как волны тепла или холода.Мы запускаем модель в течение 10 000 лет с постоянным (только зависящим от широты) воздействием, создавая неравновесные (из-за принудительно-диссипативной природы модели) стационарные симуляции без орографии, годового или суточного цикла. Форсирование симметрично для двух полушарий. Разрешение по горизонтали составляет T 42 с десятью вертикальными уровнями, а значения температуры записываются ежедневно. Мы вычисляем и сравниваем перенормированные функции скорости на основе интегрированной автокорреляции для временных и зональных температурных последовательностей на выбранных широтах (60 °, 46 ° и 30 °), уделяя особое внимание области средних широт, где турбулентность является наилучшей. развитый.Пространственное усреднение выполняется только в зональном направлении, поскольку это геометрическое направление, вдоль которого система имеет симметрию. Мы также анализируем двумерный случай, т.е. пространственно-временное усреднение. Мы проверяем правильность наших результатов, сравнивая периоды возврата, основанные на функциях ставок, с периодами возврата из эмпирических данных и из метода пика над порогом. Прежде чем обсуждать их подробно, мы сначала резюмируем наши основные выводы:
1.
Средние значения температуры в PUMA основаны на принципе больших отклонений.
2.
Временная и зональная перенормированные функции скорости равны, если мы вычисляем их, исключая влияние временных и зональных корреляций. Таким образом, мы можем определить универсальную функцию, описывающую как временные, так и пространственные большие отклонения.
3.
Пространственно-временные перенормированные функции скорости равны универсальной функции для малых и больших длин пространственного усреднения.На промежуточных уровнях в результате нетривиальной пространственной корреляции пространственно-временные перенормированные функции скорости отличаются от универсальных.
Расчетные функции скорости явно сходятся в случае временных средних. Мы получаем надежные оценки при оптимальной длине усреднения, которая составляет около, где представляет временную интегрированную автокорреляцию. Тот факт, что мы находим принцип больших отклонений для средних значений температуры, может показаться неудивительным, но на самом деле это имеет чрезвычайно важные последствия на практическом уровне.Основываясь на больших отклонениях, мы можем оценить вероятности средних значений и, таким образом, для практического использования очень важные периоды возврата для каждой длины усреднения. Все, что нам нужно знать, — это вероятность средних значений, которую мы можем оценить эмпирически. В отличие от временных средних, в случае зонального усреднения длина пространственного усреднения n x существенно ограничена размером и формой широтного круга. Временное усреднение выполняется на теоретически бесконечной (и практически очень длинной) линии, тогда как зональное усреднение происходит на окружности.Таким образом, сходимость оценочных функций ставок не так очевидна, как для временных средних. Однако сравнение результатов по зонам с повторными нормированными по времени оценками функции скорости показывает, что длина усреднения, по-видимому, обеспечивает разумную оценку функции скорости, поэтому мы выбираем ее в качестве оптимальной длины зонального усреднения. В случае 30 ° широты достичь невозможно из-за более сильных зональных корреляций. Здесь максимальная длина усреднения составляет.
Мы находим, что временные и пространственные повторно нормализованные функции скорости кажутся равными, если мы устраняем эффект корреляций в соответствии с уравнением (20), где мы в основном масштабируем функции скорости на количество некоррелированных данных вместо всего количества. данных в блоке усреднения.На основе этой эквивалентности можно найти универсальную функцию в том смысле, что она описывает большие отклонения как во времени, так и в пространстве. С практической точки зрения это означает, что можно перемещаться между пространством и временем: мы можем вывести статистические свойства пространственных средних (включая оценки уровня доходности) из одного временного ряда, и это, конечно, верно в обратном направлении. тоже.
Очевидно, что на основе предела большого отклонения, полученного в одном измерении — времени или пространстве, — мы не можем описать устойчивые события, потому что закон предела действует в очень больших масштабах, где пространственная или временная организация теряется и возникает универсальность.Однако, как показывают наши результаты, устойчивые пространственно-временные события можно изучать на основе LDT, если выполнять усреднение в обоих измерениях — времени и пространстве.
Таким образом, мы расширяем наш анализ также на большие пространственно-временные отклонения. Здесь мы сначала усредняем в зональном направлении, принимая разные длины усреднения, а затем ищем принцип большого отклонения во времени для зонально усредненных наблюдаемых. Мы обнаружили, что пространственно-временная перенормированная функция скорости, вычисленная снова путем исключения корреляций согласно (22), равна универсальной функции I n в двух случаях: (1) для небольшого зонального усреднения длины и (2) для больших.Мы предполагаем, что в первом случае из-за малого значения n x , усредненная по зонам наблюдаемая существенно не отличается от временной наблюдаемой, и, таким образом, функция скорости сходится к универсальной функции. Во втором случае средние по зонам уже демонстрируют универсальные характеристики, потому что большие n x допускают достаточное смешивание в серии средних по зонам. Эти универсальные характеристики не изменяются дополнительным временным усреднением.Однако в промежуточных масштабах, то есть из-за нетривиальных зональных корреляций, после зонального усреднения получается совершенно другая наблюдаемая, большие отклонения которой следуют за функцией скорости, явно отличной от универсальной. Следовательно, вычисляя большие отклонения во времени зональных средних значений, мы избавляемся от временной устойчивости, если временная длительность усреднения достаточно велика, но мы не можем исключить эффект зональной устойчивости на промежуточных масштабах, что затем приводит к неуниверсальной повторной оценке. нормализованная функция скорости.Это также означает, что таким образом мы можем изучать устойчивые экстремальные явления на основе LDT. Эти промежуточные масштабы около 5–10 или 2000–4000 км примерно равны масштабам стойких синоптических возмущений, подобных тем, которые вызывают сильные волны тепла. Согласно этой точке зрения, длительные нарушения синоптического масштаба — это большие отклонения от устойчивого состояния, которые допускают более высокую степень пространственно-временной организации и, в широком смысле, более низкую энтропию по сравнению с возмущениями любого другого масштаба.Это интересный признак так называемой низкочастотной изменчивости атмосферы, которая проявляется в сложной феноменологии, как в случае блокирующих событий (Tibaldi and Molteni 2018).
Преимущество применения LDT для анализа устойчивых климатических явлений заключается, помимо уже обсуждавшейся предсказательной силы, в возможности узнать кое-что об исследуемой системе:
- Наша система достаточно хаотична, чтобы учесть принцип больших отклонений.Это означает, что корреляции затухают достаточно быстро, и система достаточно перемешивается, чтобы гипотеза хаотичности оставалась верной. Очень важной характеристикой систем такого типа является то, что в флуктуациях преобладает среднее значение, а не самые большие события, и, таким образом, выполняется центральная предельная теорема.
- Скоростные функции приблизительно симметричны, так что положительные колебания и соответствующие отрицательные колебания одинакового размера имеют одинаковую вероятность возникновения.
- Мы получаем эквивалентность временных и пространственных перенормированных функций скорости, что означает, что флуктуации во времени эквивалентны флуктуациям в пространстве, если принять во внимание различные пространственные и временные масштабы.Таким образом, наша неравновесная стационарная система демонстрирует симметрию между временным и пространственным (зональным) измерениями. Это говорит о том, что в перенормированных временном и пространственном измерениях статистические свойства температуры можно рассматривать как изотропные.
- Мы обнаружили, что пространственно-временная функция скорости, относящаяся к промежуточным пространственным масштабам, существенно более плоская и ниже универсальной функции. Следовательно, большие отклонения в нашей системе более вероятны в промежуточных пространственных масштабах, чем в любом другом масштабе.
Кроме того, мы сравниваем две схемы для исследования редких событий, то есть LDT и подход теории экстремальных значений «пик над порогом», с практической точки зрения, основанный на оценках уровня доходности и периода повторяемости. Оба метода основаны на предельных законах, но они различаются способом получения предела и, следовательно, направлением действия предела. Подход «пик над порогом» имеет дело с условными вероятностями среднего превышения высокого порога.Предельный закон получается при рассмотрении все больших и больших экстремумов, таким образом, он направлен на большие, даже ненаблюдаемые события. В случае LDT мы приближаемся к пределу, поскольку мы рассматриваем средние значения с увеличением длины усреднения n , таким образом, предел направлен в сторону. Наши результаты указывают на эти различия. С одной стороны, оценки уровня доходности, основанные на теории больших отклонений, ограничены сверху при малых длинах усреднения, поскольку они получены на основе эмпирических распределений, тогда как оценки, основанные на подходе «пик над порогом», могут быть экстраполированы на ненаблюдаемые события.С другой стороны, уровни доходности, основанные на больших отклонениях, могут быть получены для каждого на основе вероятностей, тогда как в случае подхода «пик выше порога» они должны оцениваться для каждых n отдельно. Мы также должны отметить, что сходимость к предельному закону, кажется, легче достичь в случае больших отклонений, чем в случае экстремальных значений (Gálfi et al 2017).
Как упоминалось выше, мы устраняем эффект корреляции при вычислении функций скорости умножением с интегрированной автокорреляцией.Мы оцениваем как временные, так и зональные интегрированные автокорреляции, и. Вычисляя соотношение между пространственной и временной устойчивостью, мы определяем масштабную скорость, которая является мерой анизотропии между пространством и временем. Если анизотропия между пространством и временем велика, становится труднее показать существование универсальной функции скорости, как в случае широты 30 °. Заметим, что масштабную скорость, которую мы находим с помощью такой асимптотической процедуры, можно рассматривать в связи с направлениями исследований, направленных на выявление мультифрактальной природы полей погоды и климата (Lovejoy, Schertzer 2013) и, в частности, полей осадков (Deidda 2000).Обычно связь между пространственным и временным масштабами задается некоторой характеристической скоростью. В мультифрактальном анализе пространственно-временных полей осадков временное измерение обычно масштабируется на скорость адвекции, чтобы соответствовать пространственным, как объяснил Дейдда (2000). Если масштабированные временные и пространственные измерения изотропны, общей адвективной скорости достаточно для описания взаимосвязи между пространственными и временными свойствами поля осадков.Однако в случае пространственно-временной анизотропии адвективная скорость зависит от масштаба. В этой работе мы ищем связь между временем и пространством в терминах функций скорости и обнаруживаем, что эта пространственно-временная связь очень хорошо описывается соотношением пространственной и временной интегрированной автокорреляции, которое мы обозначаем как. Как упоминалось в разделе 4, она сравнима со средней зональной скоростью на широтах 60 ° и 46 °, которая действительно адвектирует турбулентные структуры в первом приближении.Однако при 30 ° согласие хуже. В этом случае динамика имеет смешанный тропический / внетропический характер, а длительные пространственные корреляции обусловлены наличием нисходящего потока ячеек Хэдли.
Хотя природа и общество обычно не соответствуют гипотезам теорем, необходимых для установления универсальных законов, такие асимптотические результаты, тем не менее, могут быть чрезвычайно полезны для изучения данных наблюдений, как и в широко используемом случае теории экстремальных значений. Таким образом, эту работу следует рассматривать как первый шаг к использованию LDT для анализа фактических климатических данных и результатов современных климатических моделей.Перспектива состоит в том, чтобы найти новые способы эффективной оценки вероятности возникновения чрезвычайно редких событий, связанных с устойчивыми климатическими условиями. В этой работе мы сосредоточились на временных масштабах, которые длиннее, чем те, которые типичны для атмосферы, но можно применить те же методы для изучения устойчивых явлений многолетних масштабов, где вместо этого существенна изменчивость океана. Это потенциально имеет большое значение для решения проблемы оценки устойчивости человека и окружающей среды к низкочастотной изменчивости климатической системы.
В случае применения новейших моделей моделирования или данных наблюдений приходится иметь дело с различными сложностями, которые отсутствуют в наших моделированиях идеализированных моделей. В основном это связано с наличием нестационарности во временных рядах — в результате, например, сезонного цикла и, в более длительных временных масштабах, изменения климата, а также наличия нескольких временных масштабов в климатической системе, что может привести к медленному спаду корреляций для некоторых переменных.Обратите внимание, что, например, температура поверхности океана декоррелирует медленнее, чем температура поверхности суши, в результате большей теплоемкости активного поверхностного слоя в океане. Как обсуждалось выше в разделе 2, сильные корреляции могут препятствовать сходимости к предельному закону, по крайней мере, когда рассматриваются наборы данных конечного размера. Прагматические подходы к работе с системами, зависящими от времени, могут быть адаптированы из того, что было сделано в случае анализа, основанного на теории экстремальных значений. Можно исключить долгосрочный тренд, а затем посмотреть данные без тренда с помощью LDT.Аналогичным образом можно исключить годовой цикл из временного ряда, получить принцип большого отклонения и учесть годовую модуляцию позже при оценке уровней доходности. Другой возможностью было бы разделить временной ряд по сезонам и получить отдельные функции ставок для отдельных сезонов. Кроме того, было бы также труднее получить универсальные свойства больших отклонений из-за высокой пространственной неоднородности как эффекта орографии. Однако мы ожидаем, что такая универсальность должна быть найдена в регионах со схожими орографическими и климатическими характеристиками.
На основе нашего идеализированного моделирования оценочные функции скорости для температурных полей симметричны, что предполагает, что положительные большие отклонения температуры имеют такую же вероятность, что и отрицательные. Однако в более реалистичных наборах данных мы ожидаем чаще обнаруживать асимметричные функции скорости. Аргумент, подтверждающий такую гипотезу, состоит в том, что положительные большие отклонения температуры воздуха должны отличаться от отрицательных при наличии влажных процессов из-за различных химических и физических характеристик теплого воздуха по сравнению с холодным воздухом, который имеет гораздо более низкое содержание водяного пара.На самом деле может быть интересно сравнить функции скорости больших отклонений температуры поверхности с функциями температуры по влажному термометру, которая учитывает присутствие влаги и актуальна для оценки теплового стресса (Zahid et al 2017). Альтернативный способ объединения информации о температуре и влажности — посмотреть на так называемую эквивалентную потенциальную температуру, которая пропорциональна логарифму удельной энтропии воздуха (Holton 2004). Еще одна многообещающая область применения LDT к геофизическим данным связана с оползнями, вызванными атмосферными осадками, в горных районах, где стандартный подход к моделированию — это превышение порогового значения, определяемого суммарной интенсивностью и продолжительностью осадков (Keefer et al 1987, Peruccacci и др. 2017, Рагно и др. 2018).Мы оставим изучение этих направлений для будущих исследований.
История, источники, ссылки и указатели
Хьюго Тушетт: Теория больших отклонений: история, источники, ссылки и указателиИсторические документы
Математика
- H. Cramér, Sur un nouveau théorème limite dans la théorie des
probabilités, 1938. Google
книги
Французская копия | Параллельный перевод с комментарием - Санов И. Н., О вероятности больших отклонений случайных
магнитуды, 1957.
Русский оригинал | английский перевод - С. Р. С. Варадхан, Асимптотика вероятности и дифференциальные уравнения, 1966.
- Д. Плачки, Дж. Стейнебах, Теорема о
вероятности больших отклонений с приложением к теории массового обслуживания,
1975.
- М. Д. Донскер и С. Р. С. Варадхан, Асимптотическая оценка определенные ожидания марковского процесса на большое время, 1975 и 1976 гг. Часть Я | Часть II | Часть III | Часть IV
- J. Gärtner, На большом отклонения от инвариантной меры, 1977.
- Р. Р. Бахадур и С. Л. Забелл, Большой
отклонения выборочного среднего в общих векторных пространствах, 1979.
JSTOR | Евклид - A. Martin-Löf, A
Аппроксимация Лапласа для сумм независимых случайных величин,
1982.
- Р. С. Эллис, Большой
отклонения для общего класса случайных векторов, 1984. JSTOR | Евклид | pdf
- Э. Больтаузен, Лаплас
аппроксимации сумм независимых случайных векторов, 1986.
Физика
Книги
- А.Дембо и О. Зейтуни,
Большие отклонения
Методы и приложения, Springer, 1998.
Springer | Амазонка | Google книги - Ф. ден Холландер,
Большие отклонения, Монография Института Филдса, AMS,
2000.
AMS | Амазонка | Google книги - S. R. S. Varadhan, Большой Отклонения и приложения, SIAM, 1984. SIAM | Google книги
- Р. С. Эллис, Энтропия, Большие отклонения и Статистическая механика, Springer, 1985. Springer. | Амазонка
- Дж. Д. Деушель и Д.W. Строок, Большие отклонения, Academic Press, 1989. Amazon | Google книги
- Дж. Фенг, Т. Г. Курц, Большие отклонения для стохастики.
процессы, 2005. AMS
| Амазонка
- М. И. Фрейдлин, А. Д. Вентцель, Случайные возмущения.
динамических систем, Springer, 1984.
Springer | Амазонка | Google книги - J. A. Bucklew, Large Техники отклонения в Решение, моделирование и оценка, Springer, 1990. Springer | Амазонка | Google книги
- А. Шварц, А.Вайс, Большие отклонения для Анализ производительности: очереди, коммуникации и вычисления, CRC, 1995. CRC | Амазонка | Google книги
Обзоры и отзывы
Математика
- S. R. S. Varadhan, Large отклонения и энтропия, 2008. Евклид | pdf
- S. Ramasubramanian, Large
отклонения: Введение в премию Абеля 2007 г., 2008 г.
- Дж. Т. Льюис и Р. Рассел, An введение в большие отклонения для инженеров телетрафика, 1996.
- A.-S. Снитман, Большие изменения, 1986. Numdam
| pdf
- А. Аманн и Х.
Атманспахер, Вводный
примечания
по статистике больших отклонений, 1999.
- П. Балди, Ан Введение в теорию больших отклонений, 1986.
- Р. В. Рой, Шум возмущения нелинейных динамических систем, 1993.
- P. Mörters, Large теория отклонений и приложения, 2008.
- С. Робертсон и К. Почти, Большой принципы отклонения, 2010.
- H. Touchette, Базовый
введение в большие отклонения: теория,
приложения, моделирование, 2011.
Физика
- Р.
С. Эллис, Ан
обзор
теории больших
отклонения и приложения к статистической механике, 1995.
Taylor И Фрэнсис | pdf - Р. С. Эллис, Теория из большой отклонения: от расчета Больцмана 1877 г. до равновесие макросостояния в двумерной турбулентности, 1999. Physica D | pdf
- Y. Oono, Large отклонение и статистическая физика, 1989.
- Р. С. Эллис,
теория больших уклонений и приложения к статистической механике,
2008.
- Р. Грэм, Макроскопические потенциалы, бифуркации и шум в диссипативные системы, 1989. Springer | ЧАШКА
- Д. Г. Лучинский, П. В. Э. Мак-Клинток, М. И. Дикман, Аналоговые исследования нелинейные системы, 1998.
- H. Touchette, Большой девиативный подход в статистической механике, 2009.
Предметные указатели
- Введение в теорию больших уклонений
- Подробнее о математике теории больших уклонений
- Статистическая механика равновесия
- Системы дальнего действия
- Неравновесные системы
- Предел низкого уровня шума (теория Фрейдлина-Вентцелля-Грэма)
- Р.Грэхем, Макроскопические потенциалы, бифуркации и шум в
диссипативные системы, 1989.
Springer | ЧАШКА - Взаимодействующая частица
системы и макроскопическая (или гидродинамическая) теория флуктуаций
- Мультифракталы
- Соотношение колебаний
- Случайные блуждания в случайных средах
- Взаимодействующие диффузии (предел Маккина-Власова)
- Квантовые системы
- Х. Тушетт, Источники квантовых больших отклонений.pdf
- Моделирование больших отклонений
Биографии
Семинары и конференции
Разное
- Большой теория отклонений в Википедии
- выпуклый анализ в Википедии
- Legendre-Fenchel преобразовать в Википедии
- W. Fenchel, On
сопряженные выпуклые функции, 1949.
- Х. Тушетт, Лежандр-Феншель вкратце преображает, 2005.
- Х. Тушетт, Заметки о большом
отклонения, 2013.
- М. Кац, Нефтяные заметки о случайных процессах, 1956. pdf
- М. Кац, Пизанские лекции по интегрированию в функциональных пространствах и некоторых других of its Applications, 1980. pdf .
Исторические отрывки
- Выдержка из статьи Больцмана 1877 года (см. Ссылку выше), показывающая энтропию M (более именно, за вычетом энтропии), выраженную как функцию значение занятости w_i i-го уровня энергии и два ограничения (количество частиц n и энергия L), используемые для максимизации энтропии (соответственно минимизируя M).Больцман использует букву l для обозначения натурального логарифма: .
- Выдержка из статьи Эйнштейна 1910 г. (см. Ссылку выше) на критическая опалесценция, показывающая его формулу для вероятности макросостояние выражается как экспонента энтропии:
- Выдержка из статьи Санова 1957 года (см. Ссылку выше) с его основной теоремой, обнаруженная Больцмана 80 лет назад!
- Марк Кац в гл. 9 из его конспектов лекций в Пизе, 1980 г .: «Это […]
Раздел посвящен краткому знакомству с недавними работами
Донскер и Варадхан, что, на мой взгляд, самое интересное и
новаторская разработка в области функциональной интеграции с
преобладание предмета в начале пятидесятых ».
Google книги | pdf
Авторские права © HT 2016
Подход больших отклонений в статистической механике
Abstract
Теория больших отклонений занимается экспоненциальным убыванием вероятностей больших флуктуаций в случайных системах.Эти вероятности важны во многих областях исследований, включая статистику, финансы и инженерию, поскольку они часто дают ценную информацию о больших колебаниях случайной системы вокруг ее наиболее вероятного состояния или траектории. В контексте равновесной статистической механики теория больших отклонений обеспечивает экспоненциальные оценки вероятностей, которые уточняют и обобщают теорию флуктуаций Эйнштейна. В этом обзоре исследуется эта и другие связи между теорией больших уклонений и статистической механикой, чтобы показать, что математический язык статистической механики является языком теории больших уклонений.В первой части обзора излагаются основы теории больших уклонений и разрабатываются многие ее классические приложения, связанные с суммами случайных величин и марковскими процессами. Вторая часть рассматривает многие проблемы и результаты статистической механики и показывает, как они могут быть сформулированы и получены в контексте теории больших отклонений. Рассматриваемые проблемы и результаты охватывают широкий круг физических систем, включая равновесные системы многих частиц, динамику с шумовыми возмущениями, неравновесные системы, а также мультифракталы, неупорядоченные системы и хаотические системы.Этот обзор также охватывает многие фундаментальные аспекты статистической механики, такие как вывод вариационных принципов, характеризующих равновесные и неравновесные состояния, нарушение преобразования Лежандра для невогнутых энтропий и характеристика неравновесных флуктуаций через флуктуационные соотношения.
PACS
05.20.-y
65.40.Gr
02.50.-r
05.40.-a
Рекомендуемые статьи Цитирующие статьи (0)
Полный текстCopyright © 2009 Elsevier B.V. Все права защищены.
Рекомендуемые статьи
Ссылки на статьи
Большие отклонения
Большие отклонения
13 мая 2021 10:29Предельные теоремы теории вероятностей — слабые и сильные законы больших чисел, центральная предельная теорема и т. д. — в основном говорят, что средние значения, взятые на больших выборках (хорошо себя независимых, одинаково распределенных случайных величин) сходятся на ожидании значения. (Сильный закон больших чисел утверждает почти верную сходимость, центральная предельная теорема утверждает своего рода сходимость по распределению и т. д.) Эти результаты мало или ничего не говорят о скорости сходимости , однако, что часто важно для многих приложений теории вероятностей, например, статистическая механика. Один из способов решения это теория больших отклонений. (Я считаю, что терминология восходит к к Варадхану в 1970-х, но это просто впечатление, а не исследование.)
Позвольте мне сначала сказать небрежно, чтобы идея реализовалась, а потом еще
именно так, чтобы люди, знающие предмет, не слишком расстраивались.{-nr (\ epsilon)} ~.
\]
(Функция оценки должна подчиняться некоторой разумной, но технической преемственности
условий.) Это большой результат отклонения , потому что разница
между эмпирическим средним и математическим ожиданием остается постоянным как $ n $
растет — должен быть более крупный заговор, так сказать, среди
образцы, чтобы таким же образом отклоняться от ожиданий. Теперь один
причина того, что я сказал, на самом деле недостаточно, чтобы удовлетворить математика, заключается в том, что
правая часть сходится к нулю, поэтому функциональный вид
вероятность может быть чем угодно, что также сходится к нулю, и это было бы
доволен, но мы хотим выделить экспоненциальную сходимость .Обычный
Способ состоит в том, чтобы посмотреть на предельную скорость роста вероятности. Также мы хотим
вероятность того, что разница между эмпирическим средним и
ожидание попадает в любой произвольный набор. Таким образом, обычно можно увидеть, что LDP утверждается
в некоторой форме, например, для любого разумного набора $ A $, \ [
\ lim_ {n \ rightarrow \ infty} {- \ frac {1} {n} \ log {\ mathrm {Pr} \ left (\ left |
\ mathbf {E} X — S_n \ right | \ in A \ right)}} = \ inf_ {x \ in A} {r (x)} ~.
\]
(На самом деле, если быть полностью честным, я действительно не должен предполагать
что у этих вероятностей есть предел.Вместо этого я должен подключить лим
inf этого выражения в точную нижнюю грань функции скорости по внутренней части
$ A $, а ограничение на нижнюю грань функции скорости по замыканию
$ A $.)
Подобные принципы больших отклонений могут быть сформулированы для эмпирических распределение, эмпирический процесс, функционалы от траекторий выборки и т. д., скорее чем просто эмпирическое среднее. Есть уловки для привязки LDP к объекты более высокого уровня, такие как эмпирическое распределение по траекториям, к LDP на объектах более низкого уровня, как эмпирические средства.(Они идут под такими именами, как «принцип сжатия».)
Поскольку эргодическая теория расширяет вероятностные предельные законы к стохастическим процессы, а не просто последовательности независимых переменных, он неудивительно, что принципы большого отклонения справедливы и для некоторых случайные процессы. Меня особенно интересуют LDP для марковских процессов и их приложений. Там другие важные связи теории информации, поскольку в ужасном Во многих ситуациях функция коэффициента больших отклонений — это функция Кульбака-Лейблера. расхождение, а.к.а. относительная энтропия.
Связанные, но, строго говоря, отдельные темы:
- Неравенства отклонения конечной выборки, такие как неравенства Бернштейна, Чернова и Хёффдинга, которые ограничивают вероятность отклонения средних значений от ожидаемых значений более чем на определенную величину при заданных конечных размерах выборки;
- Концентрация меры, грубо говоря, верхние границы вероятностей отклонения, удерживаемые равномерно по большие классы функций. (Обратите внимание, что принципы больших отклонений соответствуют верхней и нижней границам и должны выполняться только асимптотически.)
См. Также: Экспоненциальные семейства вероятностных мер; Теория информации, большие отклонения и статистика Максимальная энтропия
- Рекомендуемое, большое изображение:
- Джеймс Баклью, Методы большого отклонения при принятии решений, Моделирование и оценка
- Томас Кавер и Джой Томас, Элементы информации Теория [Очень хорошая глава о больших отклонениях для последовательностей IID]
- Амир Дембо и Офер Зейтуни, Методы больших отклонений и Приложения [главы 2, 4 и 5, а также части главы 6, доступны в формате postscript через проф.Страница Дембо для его курс на большие отклонения]
- Франк ден Холландер, Большие отклонения [Красиво, коротко вводный текст для людей с прикладным вероятностным фоном.]
- Ричард С. Эллис
- «Теория больших отклонений: из Больцмана 1877 г.» Расчет равновесных макросостояний в двумерной турбулентности », Physica Д 133 (1999): 106—136
- Энтропия, большие отклонения и статистические данные Механика
- М.И. Фридлин, А. Д. Вентцель, Случайные возмущения Динамические системы
- Хьюго Тушетт, «Подход больших отклонений к статистической Механика », Physics Reports 478 (2009): 1–69, arxiv: 0804.0327
- С. Р. С. Варадхан, «Большой» Отклонения », Летопись Вероятность 36 (2008): 397-419, arxiv: 0804.2330 [Лекция Уолда за 2005 г.]
- Рекомендуется, крупные планы:
- Ф. Альтарелли, А. Браунштейн, Л.Далл’Аста и Р. Зеккина, «Большие отклонения каскадных процессов на графах», Physical Review E 87 (2013): 062115, arxiv: 1305.5745 [См. комментарии в разделе «Социальное заражение, информационные каскады, распространение инноваций и т. д.»]
- Р. Р. Бахадур, Некоторые предельные теоремы в статистике [1971. Обозначения теперь намного более прозрачны, и доказательства многих основные теоремы значительно упрощены. Но если есть лучший источник статистических приложений, чем эта маленькая книга, я еще не нашел ее.]
- Жюльен Барре, Фредди Буше, Тьерри Доксуа и Стефано Руффо, «Методы больших отклонений, применяемые к системам с большим радиусом действия. взаимодействия «, cond-mat / 0406358 = Статистический журнал Физика 119 (2005): 677-713
- Мишель Бенаин и Йорген В. Вейбулл, «Детерминистический Аппроксимация стохастической эволюции в играх », Econometrica 71 (2003): 879–903 [JSTOR]
- Даниэль Беренд, Питер Харремоэс, Арье Конторович, «Минимальное KL-расхождение на дополнениях шаров L1», arxiv: 1206.6544
- Кристиан Боргс, Дженнифер Чейес и Дэвид Гамарник, «Конвергент» последовательности разреженных графов: большие отклонения подход «, arxiv: 1302.4615 [См. в пределах графика]
- Ариджит Чакрабарти, «Влияние усечения на большие отклонения для случайных векторов с тяжелым хвостом», arxiv: 1107.2476
- Сурав Чаттерджи и С. Р. С. Варадхан, «Принцип больших отклонений для случайного графа Эрдоша-Реньи», arxiv: 1008.1946
- J.-R. Chazottes и D. Gabrielli, «Большие отклонения для эмпирических энтропии гиббсовских источников », математ.PR / 0406083 = Нелинейность 18 (2005): 2545—2563 [Это очень крутой результат, показывает, что энтропия блоков и скорости энтропии, оцененные по этим блокам, подчиняются принцип большого отклонения даже при увеличении длины блоков с объемом данных, при условии, что длина блока не растет слишком быстро (только логарифмически). Хотел бы я писать такие статьи.]
- W. De Roeck, Christian Maes и Karel Netocny, «H-теоремы из Автономные уравнения «, cond-mat / 0508089 [this в основном выводит H-теорему статистической механики как большие отклонения результат, принимая некоторую разумную марковскую форму для макроскопического динамика.Фактически, у нас есть отдельный аргумент, что у вас нет . эта марковская форма, вы просто недостаточно стараетесь; глянь сюда]
- Поль Дюпюи, «Анализ больших отклонений некоторых рекурсивных Алгоритмы с зависящим от состояния шумом », Annals of Probability 16 (1988): 1509–1536 [Открытый доступ]
- Поль Дюпюи и Ричард С. Эллис, Подход слабой конвергенции к теории больших уклонений [Препринт PDF]
- Грегори Л.Эйинк
- «Принцип действия в неравновесной статистической динамика », Physical Review E 54 (1996): 3419-3435 [Наименьшее действие как следствие марковской LDP]
- «Вариационная формулировка оптимального нелинейного Оценка, физика / 0011049 [Хорошая связь между оценкой оптимального состояния (если принять известную форму для лежащий в основе случайный процесс), неравновесная статистическая механика и теория больших отклонений, приводящая к понятным на вид численным схемам для оценка.]
- Джин Фенг и Томас Г. Курц, Большие отклонения для стохастика Процессы [ В сети]
- Р. Л. Каутц
- К. М. Ньюман, Дж. Э. Коэн и К. Кипнис, «Неодарвинистская эволюция подразумевает прерывистое равновесие», Nature 315 (1985): 400-401
- Энцо Оливьери и Мария Эулалия Варес, Большие отклонения и Метастабильность
- Стивен Ори и Стефан Пеликен, «Принципы больших отклонений для стационарные процессы », Анналы вероятностей 16 (1988): 1481—1495
- Эрик Смит, «Принципы больших уклонений, стохастический эффективный действия, энтропии пути, а также структура и значение термодинамических описания », arxiv: 1102.3938
- Эрик Смит и Суприя Кришнамурти, «Симметрия и коллективные флуктуации в эволюционных играх», рабочий документ SFI 11-03-010
- Хьюго Тушетт, «Асимптотическая эквивалентность вероятностных мер и случайных процессов», arxiv: 1708.02890
- Читать:
- Пол Х. Алгоет и Брайан Х. Маркус, «Теоремы о больших уклонениях для Эмпирические типы цепей Маркова, ограниченные тонкими множествами », IEEE Транзакции по теории информации 38 (1992): 1276—1291
- Абдельхамид Амрун, «Состояния равновесия для гладких отображений», arxiv: 1004.2577
- Алексей Андреанов, Джулио Бироли, Жан-Филипп Бушо и Александр Лефевр, «Теории поля и точные стохастические уравнения для взаимодействующая частица системы », Физическая Обзор E 74 (2006): 030101, cond-mat / 0602307
- Дэвид Андриё, «Классы эквивалентности для больших отклонений», arxiv: 1208.5699
- Эллен Бааке, Франк ден Холландер и Натали Зинт, «Как Т-клетки используют Большие отклонения от признания иностранного Антигены », arxiv: q-bio.SC/0605016 [Предположительно == статья с таким же названием в журнале Journal of Mathematical Biology 57 (2008): 841-861, но это заказывает авторов Зинт, Бааке и ден Холландер.]
- Дж. Баррал и П. Гонсалвес, «Об оценке спектра больших отклонений», Journal of Statistical Физика 144 (2011): 1256—1283
- Л. Бертини, А. Де Соле, Д. Габриэлли, Дж. Йона-Лазинио, К. Ландим, «Подход с большими отклонениями к неравновесным процессам в стохастических решеточных газах», arxiv: math / 0602557
- Маттиас Биркнер, Андреас Гревен и Франк ден Холландер, «Принцип подавления большого отклонения для слов в последовательности букв», arxiv: 0807.2611
- Игорь Белакович, Жан-Доминик Деушель, Тилль Крюгер, Руеди Зайлер, Райнер Зигмунд-Шульце и Арлета Школа
- Амарджит Будхираджа, Пол Дюпюи, Маркус Фишер, «Свойства больших уклонений слабо взаимодействующих процессов с помощью методов слабой сходимости», arxiv: 1009.6030
- Amarjit Budhiraja, Paul Dupuis, Vasileios Maroulas, «Большой» отклонения для бесконечномерных стохастических динамических систем », Анналы. прикладной вероятности 36 (2008): 1390—1420, arxiv: 0808.3631
- Адриан А. Будини, «Большие отклонения эргодических процессов подсчета: подход статистической механики», Physical Review E 84 (2011): 011141, arxiv: 1112.2625
- Патрик Каттьо и Натэль Гозлан, «Границы отклонений и условные принципы для тонких множеств», arxiv: math / 0510257
- Рафаэль Серф и Пьер Пети, «Теорема Крамера для асимптотически разделенных полей», arxiv: 1103.4415 [Аннотация на английском языке чрезвычайно интересна, но, к сожалению, эта статья на французском языке, поэтому моя отметка «для чтения» вводит в заблуждение.]
- Ариджит Чакрабарти, «Центральная предельная теорема и большие отклонения для усеченных случайных векторов с тяжелым хвостом», arxiv: 1003.2159
- Hanshuang Chen, Feng Huang, Guofeng Li, Haifeng Zhang, «Большие отклонения и аномальные флуктуации, масштабируемые в степени ассортативности в конфигурационных сетях», arxiv: 1907.13330
- Джихеок Чой и Сандер Сетураман, «Большие отклонения для структуры степеней в схемах предпочтительной привязанности», Анналы прикладной вероятности 23 (2013): 722-763
- По-Нинг Чен, «Обобщение теоремы Гартнера-Эллиса», транзакций IEEE на Теория информации 46 (2000): 2752—2760
- Чжи Чи
- Альберто Кьярини, Маркус Фишер, «О больших отклонениях для процессов Ито с малым шумом», Успехи в прикладной теории вероятностей 46 (2014): 1126-147, arxiv: 1212.3223
- Игорь Чуешов и Анни Милле, «Стохастические 2D гидродинамические системы: корректность и большие отклонения», arxiv: 0807.1810
- А. де Акоста, «Общий невыпуклый результат большого отклонения II », Анналы вероятностей 32 (2004): 1873–1901, math.PR/0410101
- Зак Дейтц и Сандер Сетураман, «Большие отклонения для класса неоднородные цепи Маркова », math.PR/0404230
- Франк ден Холландер, Жюльен Пуазат, «Принципы больших отклонений для слов, взятых из коррелированных последовательностей букв», arxiv: 1303.5383
- Б. Деррида, «Неравновесные стационарные состояния: флуктуации и большие отклонения плотности и ток «, cond-mat / 0703762
- Б. Деррида, Джоэл Л. Лебовиц и Юджин Р. Спир, «Exact Large Функционал отклонения для профиля плотности в стационарной неравновесности Открытая система, «cond-mat / 0105110
- Ман Хонг Зыонг, Марк А. Пелетье, Упаншу Шарма, «Крупнозернистость и колебания: Два зайца одним выстрелом», arxiv: 1404.1466
- Влад Эльгарт и Алексей Каменев, «Статистика редких событий в Реакция — диффузионные системы «, cond-mat / 0404241 [i.е., большой отклонения]
- Андреас Энгель, Реми Монассон и Александр К. Хартманн, «О большом Свойства отклонения случайных графов Эрдоша-Реньи », Journal of Statistical Физика 117 (2004): 387—426
- Михаил Ермаков, «Принцип умеренного отклонения для эмпирической бутстраповой меры», arxiv: 1206.1459
- Париса Фатхеддин, Цзе Сюн, «Принцип больших отклонений для некоторых процессов с измерением значений», arxiv: 1204.3501
- Марио Филиаси, Джакомо Ливан, Маттео Марсили, Мария Пересси, Эрик Весселли, Элиа Заринелли, «О концентрации больших отклонений для распределений с толстым хвостом в применении к финансовым данным», arxiv: 1201.2817
- Ханс Фоллмер и Стивен Ори, «Большие отклонения для эмпирического поля мера Гиббса », Annals of Probability 16 (1988): 961-977
- Хорхе Гарсиа, «Принцип большого отклонения для стохастика» Интегралы », Журнал Теоретическая вероятность 21 (2008): 476-501
- Кристиан Джардина, Хорхе Курчан, Лука Пелити, «Прямая оценка» большого отклонения функции », cond-mat / 0511248
- Юрий Голубев, Владимир Спокойный, «Экспоненциальные оценки для оценок минимального контраста», arxiv: 0901.0655
- Наталь Гозлан и Кристиан Леонар
- Алиса Гионне, «Большие уклонения и стохастическое исчисление для больших случайные матрицы », Вероятность Опросы 1 (2004): 72–172 [Открытый доступ]
- Гулинский О.В. и Р. С. Липцер, «Пример Большие уклонения для стационарных процессов », Теория вероятностей и Приложения 44 (1999): 211—225 [PDF]
- Те Сун Хан, «Подход с использованием информационного спектра к большим отклонениям». теоремы », cs.IT / 0606104
- Хенрик Халт и Геннадий Самородницкий, «Большие отклонения для точечных процессов на основе стационарных последовательностей с тяжелыми хвостами», Journal of Applied Probability 47 (2010): 1-40
- Сванте Янсон, «Большие отклонения сумм частично зависимых случайные величины », Random Структуры и алгоритмы 24 (2004): 234–248 [«Мы использовать и расширять метод Хёффдинга для получения сильных границ больших отклонений для сумм зависимых случайных величин с подходящей структурой зависимостей.В Метод основан на разбиении суммы на суммы независимых переменные. Подаются заявки на U-статистику, случайные строки и случайные графиков «. Применяется здесь только к случайным графам Эрдоша-Реньи (IID), но может быть расширяемый до марковского случайного графики …? PDF препринт]
- Джованни Йона-Лазинио, «От флуктуаций гидродинамики к неравновесный термодинамика », arxiv: 1003.4164
- Владислав Каргин, «Неравенство больших уклонений для вектора Функции на конечном обратимом Маркове Цепи », математ.PR / 0508538
- Герхард Келлер, Состояния равновесия в эргодической теории
- Майкл Кейл, «Квантовая оценка состояния и большие отклонения», Quant-ph / 0412053
- Юрий Кифер, «Большие уклонения и адиабатические переходы для динамических систем и марковских процессов при полностью связанном усреднении», arxiv: 0710.2405
- Юрий Кифер, С. Р. С. Варадхан, «Нетрадиционные теоремы о больших уклонениях», Теория вероятностей и связанные области 158 (2014): 197-224, arxiv: 1206.0156
- Ф. Клебанер и Р. Липцер, «Большой Отклонения для прошлозависимых Рекурсии », math.PR/0603407 [Исправленная версия Проблемы информации Коробка передач 32 (1996): 23-34]
- Иоаннис Контояннис и С. П. Мейн
- Кристиан Куен, Мартин Г. Ридлер, «Большие отклонения для нелокальных стохастических нейронных полей», Журнал математической нейробиологии 4 (2014): 1-33, arxiv: 1302.5616
- Д. Лакост, А.В. К. Лау и К. Маллик, «Теорема флуктуации и функция больших отклонений для решаемой модели молекулярного двигателя», Physical Review E 78 (2008): 011915
- Вивьен Леконт, Сесиль Аппер-Роллан и
Фредерик ван Вейланд
- «Термодинамический формализм для систем с Марков динамика », cond-mat / 0606211
- «Термодинамический формализм и функции больших уклонений в непрерывное время Марков динамика », cond-mat / 0703435
- Вивьен Леконт и Жюльен Тайлер, «Численный подход к большим отклонения в непрерывном время », Журнал Статистическая механика: теория и эксперимент 2007 : P03004
- Рафаэль Лефевере, Мауро Мариани, Лоренцо Самботти, «Большие отклонения для процессов обновления», arxiv: 1009.2659
- Кристиан Леонар, «Энтропийные проекции и доминирующие точки», ESAIM: Вероятность и статистика 14 (2010): 343-381, arxiv: 0711.0206 [«Обобщенные энтропийные проекции и доминирующие точки являются решениями проблем выпуклой минимизации, связанных с условным законам больших чисел «]
- Роберт Ш. Липцер , Анатолий А. Пухальский, «Предельные теоремы о больших уклонениях для семимартингалы », math.PR/0510028 [Но опубликовано в журнале в 1992 г.]
- Фотис Лукиссас, «Точные большие отклонения для длиннохвостых распределений», Журнал теоретической вероятности 25 (2012): 913-924
- Ютао Ма, Ран Ван, Лиминг Ву, «Принцип умеренного отклонения для динамических систем с малым случайным возмущением», arxiv: 1107.3432
- Клаудио Макчи, «Большие отклонения для эмпирических оценок стационарного распределения полумарковского процесса с конечным пространством состояний», Коммуникации в Статистика: теория и методы 37 (2008): 3077-3089
- Сатья Н. Маджумдар и Алан Дж. Брей, «Функции большого уклонения для Нелинейные функционалы гауссовского стационарного марковского процесса », Physical Review E 65 (2002): 051112, cond-mat / 0202138
- Николай Матни, Стивен Ту, «Учебное пособие по границам концентрации для идентификации системы», arxiv: 1906.11395
- Дэвид Макаллестер, «Подход статистической механики к большим Теоремы об отклонениях »[Доступна электронная печать через CiteSeer — опубликовано?]
- Томас Микош, Оливье Винтенбергер, «Точные большие отклонения для зависимых правильно меняющихся последовательностей», arxiv: 1206.1395
- Абделькадер Моккадем, Мариан Пеллетье и Баба Тиам, «Большой и принципы умеренных отклонений для ядерных оценок многомерной регрессия », math.ST/0703341
- К. Неточны, Ф.Редиг, «Большие уклонения для квантового спина. систем », Журнал статистической физики 117 (2004): 521—547, math-ph / 0404018
- Уассим Фелиачи, Фредди Буше, «Большие динамические отклонения для однородных систем с дальнодействующими взаимодействиями и уравнение Балеску — Гернси — Ленарда», arxiv: 2105.05644
- Магда Пелиград, Хайлин Санг, Юнда Чжун, Вэй Бяо Ву, «Точные умеренные и большие отклонения для линейных процессов», arxiv: 1111.0537
- Huyen Pham, «Некоторые приложения и методы больших отклонений в финансы и страхование », математ.PR / 0702473
- Марк Полликотт и Ричард Шарп, «Большие отклонения, колебания и сокращающиеся интервалы», Communications по математической физике 290 (2009): 321—334
- Анатолий Пухальский, Большие отклонения и идемпотент Вероятность
- Анатолий А. Пухальский, «Случайные процессы в случайных графах», math.PR/0402183 [Большой отклонения для графов Эрдеша-Реньи. Памятка себе: сколько работы нужно было бы распространить это на марковские графы?]
- Хун Цянь, «Относительная энтропия: свободная энергия, связанная с Колебания равновесия и неравновесие Отклонения », Физ. Обзор E 63 (2001): 042103, math-ph / 0007010
- Оливье Ривуар, «Полостной метод для больших отклонений», Журнал Статистическая механика: теория и эксперимент (2005): P07004, cond-mat / 0506164 [«Введен метод изучения больших отклонений в контексте статистическая физика неупорядоченных систем.Подход, основанный на расширении метода резонатора к нетипичным реализациям закаленного беспорядка, позволяет нам для вычисления экспоненциально малых вероятностей (функций скорости) для различных классы случайных графов. «]
- Дэвид Рюэлль, Термодинамический формализм
- Шин-ичи Саса, «Физика больших отклонений», arxiv: 1204.5584
- Л. Саулис, В. А. Статулявичюс, Предельные теоремы для больших уклонений
- Кэролайн Шредер, I-Проекция и условные предельные теоремы для марковских процессов с дискретными параметрами », Анналы вероятностей 21 (1993): 721-758
- Адам Шварц, Большие отклонения в моделировании производительности
- Джо Сузуки, «Анализ цепей Маркова генетических алгоритмов: подход на основе принципа большого отклонения», Journal of Applied Вероятность 47 (2010): 967—975
- Хьюго Тушетт, Розмари Дж.Харрис, «Подход больших уклонений к неравновесным системам», arxiv: 1110.5216
- Хосе Трашоррас, Оливье Винтенбергер, «Большие отклонения для начальных эмпирических измерений», arxiv: 1110.4620
- А. Вульпиани, Ф. Чеккони, М. Ченчини, А. Пуглиси и Д. Верни (ред.) M Большие отклонения в физике: наследие закона больших чисел
- Вэй Ван, А. Дж. Робертс и Цзиньцяо Дуань, «Большие отклонения для медленный-быстрый стохастический частный дифференциал уравнения », arxiv: 1001.4826
- Lingjiong Zhu, «Большие отклонения на уровне процесса для общих процессов Хокса», arxiv: 1108.2431
- Для записи:
- CRS, «Большие отклонения в экспоненциальных семействах стохастика» Автоматы »
Предыдущие версии : 2005-11-09 17:39 (но ни в коем случае не первая версия)
Теория больших отклонений и распределение изменений цен
Автор
Включено в список:- Laurent-Emmanuel Calvet
(GREGH — Groupement de Recherche et d’Etudes en Gestion à HEC — HEC Paris — Ecole des Hautes Etudes Commerciales — CNRS — Centre National de la Recherche Scientifique)
- Бенуа Б.Мандельброт
(Исследовательский центр IBM Томаса Дж. Ватсона — IBM, Департамент математики — Йельский университет [Нью-Хейвен])
- Адлай Дж. Фишер
(Саудер — Школа бизнеса Саудера [Британская Колумбия] — UBC — Университет Британской Колумбии)
Abstract
Мультифрактальная модель доходности активов (MMAR, см. Mandelbrot, Fisher, and Calvet, 1997) предлагает класс мультифрактальных процессов для моделирования финансовой отдачи. В этой статье мультифрактальные процессы определяются масштабным законом для моментов приращений процессов на конечных интервалах времени.В данной статье мы обсуждаем локальное поведение мультифрактальных процессов. Мы используем локальные показатели Гёльдера, фундаментальную концепцию реального анализа, которая описывает свойства локального масштабирования реализованного пути в любой момент времени. В отличие от стандартных моделей непрерывного финансирования, мультифрактальные процессы содержат множество локальных показателей Гёльдера в пределах любого конечного интервала времени. Мы характеризуем распределение показателей Гёльдера мультифрактальным спектром процесса.Для широкого класса мультифрактальных процессов это распределение может быть получено путем применения теории больших отклонений Крамера. В альтернативной интерпретации мультифрактальный спектр описывает фрактальную размерность множества точек, имеющих заданный локальный показатель Гёльдера. Наконец, мы покажем, как получить процессы с различными спектрами. Это позволяет прикладному исследователю связать эмпирическую оценку мультифрактального спектра с конкретной конструкцией стохастического процесса.
Рекомендуемая ссылка
Примечание. Просмотрите исходный документ на сервере открытого архива HAL: https://hal-hec.archives-ouvertes.fr/hal-00601869
Загрузить полный текст от издателя
Насколько нам известно, этот элемент недоступен для скачать .Чтобы узнать, доступен ли он, есть три варианты:1. Проверьте ниже, доступна ли в Интернете другая версия этого элемента.
2. Зайдите на страницу провайдера действительно ли он доступен.
3. Выполните поиск элемента с таким же названием, который был бы имеется в наличии.
Исправления
Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения. При запросе исправления укажите идентификатор этого элемента: RePEc: hal: wpaper: hal-00601869 .См. Общую информацию о том, как исправить материал в RePEc.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь:. Общие контактные данные провайдера: https://hal.archives-ouvertes.fr/ .
Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь. Это позволяет связать ваш профиль с этим элементом. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которого мы не уверены.
У нас нет библиографических ссылок на этот товар. Вы можете помочь добавить их, используя эту форму .
Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле службы авторов RePEc, поскольку там могут быть некоторые цитаты, ожидающие подтверждения.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, аннотации, библиографической информации или информации для загрузки, обращайтесь: CCSD (адрес электронной почты указан ниже).Общие контактные данные провайдера: https://hal.archives-ouvertes.fr/ .
Обратите внимание, что исправления могут отфильтроваться через пару недель. различные сервисы RePEc.
Определение стандартного отклонения
Что такое стандартное отклонение?
Стандартное отклонение — это статистика, которая измеряет разброс набора данных относительно его среднего значения. Стандартное отклонение рассчитывается как квадратный корень из дисперсии путем определения отклонения каждой точки данных относительно среднего значения.Если точки данных находятся дальше от среднего, в наборе данных имеется большее отклонение; таким образом, чем шире разброс данных, тем выше стандартное отклонение.
Ключевые выводы:
- Стандартное отклонение измеряет разброс набора данных относительно его среднего значения.
- Волатильные акции имеют высокое стандартное отклонение, в то время как отклонение стабильных голубых фишек обычно довольно низкое.
- С другой стороны, стандартное отклонение рассчитывает всю неопределенность как риск, даже если она в пользу инвестора, например, доходность выше среднего.
Понимание стандартного отклонения
Стандартное отклонение — это статистический показатель в области финансов, который в применении к годовой норме доходности инвестиций проливает свет на историческую волатильность этих инвестиций. Чем больше стандартное отклонение ценных бумаг, тем больше разница между каждой ценой и средним значением, которое показывает больший ценовой диапазон. Например, волатильные акции имеют высокое стандартное отклонение, в то время как отклонение стабильных голубых фишек обычно довольно низкое.{th} \ text {точка в наборе данных} \\ & \ overline {x} = \ text {Среднее значение набора данных} \\ & n = \ text {Количество точек данных в наборе данных} \ конец {выровнен} Стандартное отклонение = n − 1∑i = 1n (xi −x) 2, где: xi = значение i-й точки в наборе данных x = среднее значение набора данных
Расчет стандартного отклонения
Стандартное отклонение рассчитывается следующим образом:
- Среднее значение вычисляется путем сложения всех точек данных и деления на количество точек данных.
- Дисперсия для каждой точки данных вычисляется путем вычитания среднего значения из значения точки данных. Затем каждое из этих результирующих значений возводится в квадрат и суммируются результаты. Затем результат делится на количество точек данных за вычетом единицы.
- Квадратный корень из дисперсии — результат № 2 — затем используется для определения стандартного отклонения.
Использование стандартного отклонения
Стандартное отклонение — особенно полезный инструмент в инвестиционных и торговых стратегиях, поскольку он помогает измерять волатильность рынка и ценных бумаг, а также прогнозировать тенденции производительности.Например, что касается инвестирования, индексный фонд, вероятно, будет иметь низкое стандартное отклонение по сравнению с его эталонным индексом, поскольку цель фонда — воспроизвести индекс.
С другой стороны, можно ожидать, что фонды агрессивного роста будут иметь высокое стандартное отклонение от относительных фондовых индексов, поскольку их управляющие портфелями делают агрессивные ставки для получения прибыли выше среднего.
Более низкое стандартное отклонение не обязательно предпочтительнее. Все зависит от вложений и готовности инвестора принять на себя риск.Имея дело с величиной отклонений в своих портфелях, инвесторы должны учитывать свою терпимость к волатильности и свои общие инвестиционные цели. Более агрессивные инвесторы могут быть довольны инвестиционной стратегией, которая выбирает автомобили с волатильностью выше среднего, в то время как более консервативные инвесторы могут не делать этого.
Стандартное отклонение — один из ключевых фундаментальных показателей риска, который используют аналитики, управляющие портфелем, консультанты. Инвестиционные фирмы сообщают о стандартном отклонении своих паевых инвестиционных фондов и других продуктов.Большой разброс показывает, насколько доходность фонда отклоняется от ожидаемой нормальной доходности. Поскольку эта статистика проста для понимания, она регулярно предоставляется конечным клиентам и инвесторам.
Стандартное отклонение по сравнению с отклонением
Дисперсия получается путем взятия среднего значения точек данных, вычитания среднего значения из каждой точки данных в отдельности, возведения в квадрат каждого из этих результатов, а затем взятия другого среднего значения этих квадратов. Стандартное отклонение — это квадратный корень из дисперсии.
Дисперсия помогает определить размер разброса данных по сравнению со средним значением. По мере того, как дисперсия становится больше, происходит больше вариаций в значениях данных, и может быть больший разрыв между одним значением данных и другим. Если все значения данных близки друг к другу, дисперсия будет меньше. Однако это сложнее понять, чем стандартное отклонение, потому что дисперсия представляет собой результат, возведенный в квадрат, который не может быть осмысленно выражен на том же графике, что и исходный набор данных.
Стандартные отклонения обычно легче изобразить и применить. Стандартное отклонение выражается в той же единице измерения, что и данные, что не обязательно относится к дисперсии. Используя стандартное отклонение, статистики могут определить, имеют ли данные нормальную кривую или другую математическую зависимость. Если данные ведут себя по нормальной кривой, то 68% точек данных будут находиться в пределах одного стандартного отклонения от среднего или среднего значения точки данных. Большие отклонения приводят к тому, что большее количество точек данных выходит за пределы стандартного отклонения.Меньшие отклонения приводят к большему количеству данных, близких к среднему.
Большой недостаток
Самый большой недостаток использования стандартного отклонения заключается в том, что на него могут влиять выбросы и экстремальные значения. Стандартное отклонение предполагает нормальное распределение и рассчитывает всю неопределенность как риск, даже если она в пользу инвестора, например, доходность выше среднего.
Пример стандартного отклонения
Скажем, у нас есть точки данных 5, 7, 3 и 7, всего 22.Затем вы разделите 22 на количество точек данных, в данном случае на четыре, что даст среднее значение 5,5. Это приводит к следующим определениям: x̄ = 5.5 и N = 4.
Дисперсия определяется путем вычитания среднего значения из каждой точки данных, что дает -0,5, 1,5, -2,5 и 1,5. Затем каждое из этих значений возводится в квадрат, в результате получается 0,25, 2,25, 6,25 и 2,25. Значения квадратов затем складываются, в результате получается 11, которые затем делятся на значение N минус 1, что составляет 3, в результате получается дисперсия примерно 3.67.
Затем вычисляется квадратный корень из дисперсии, что дает стандартное отклонение примерно 1,915.
Или рассмотрим акции Apple (AAPL) за последние пять лет. Доходность акций Apple составила 12,49% в 2016 году, 48,45% в 2017 году, -5,39% в 2018 году, 88,98% в 2019 году и по состоянию на сентябрь 60,91% в 2020 году. 36,88%.
Таким образом, абсолютное значение годовой прибыли за вычетом среднего составляет 24.39%, 11,57%, 42,27%, 52,1% и 24,03% соответственно. Затем все эти значения возводятся в квадрат, чтобы получить 0,059, 0,013, 0,179, 0,271 и 0,058. Выборочная дисперсия — это среднее значение квадрата разности, или 0,145, где значения в квадрате складываются и делятся на 4 (N минус 1). Квадратный корень из дисперсии используется для получения стандартного отклонения 38,08%.
Институт Филдса — Аспирантура по теории больших отклонений
Вероятность тематической программы и ее применение Осень 1998
Аспирантура по теории больших отклонений: введение и применение
Инструктор: Франк ден Холландер denholla @ sci.kun.nl
Математический факультет Неймегенского университета
с 14 сентября 1998 г.
Пререквизиты: Основы теории вероятностей.
Этот курс представляет собой введение в большие отклонения и описывает как теория и приложения. Теория больших отклонений — часть вероятности, статистика и статистическая физика — занимается описанием события, при которых случайная величина отклоняется от своего среднего значения больше, чем «нормальное» количество (т.е.сверх того, что описывается центральной предельной теоремой). Точный расчет вероятностей таких событий оказывается иметь решающее значение для изучения интегралов от экспоненциальных функционалов случайных величин, которые возникают в разных контекстах.
Часть 1: Вывод некоторых элементарных теорем о больших уклонениях для i.i.d случайные величины. Здесь упор делается на явный расчет для нескольких простых примеров и понимания основных механизмов действующий.
Часть 2: Представление некоторых общих определений и теорем в
более абстрактном контексте. Здесь цель — раскрыть единую схему, которая
дает теорию больших отклонений ее общую структуру, и это может быть сделано
работать в самых разных случаях.
Часть 3: Вывод некоторых элементарных теорем о больших уклонениях для Цепи Маркова, опять же с упором на явное вычисление.
Часть 4: Описание приложений.Некоторые примеры включают: полимер цепочки, статистическая проверка гипотез и нейронные сети.
Оценка: Доступно много упражнений.
.
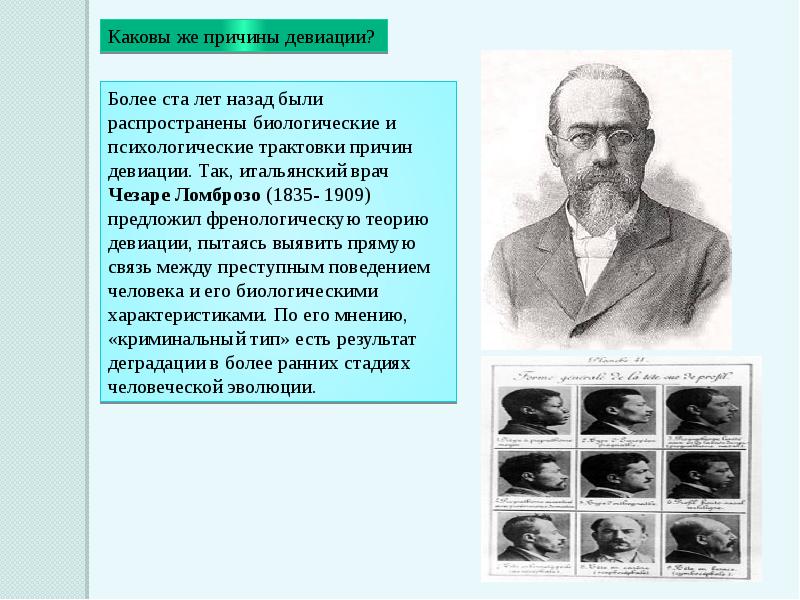
 Их девиантность заключается
в нетрадиционном стиле жизни и, что,
может быть, еще серьезнее — в их
добровольном выборе именно такой жизни.
Их девиантность заключается
в нетрадиционном стиле жизни и, что,
может быть, еще серьезнее — в их
добровольном выборе именно такой жизни.

 пособие для студентов высших учеб. заведений. — М., 2003.
пособие для студентов высших учеб. заведений. — М., 2003.